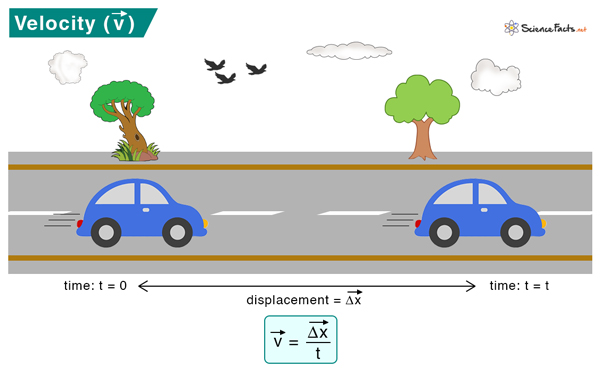
The importance of velocity is that it can give you an estimated time to go from one point to another. Suppose you are traveling from place A to place B. Velocity tells you how long it will take to arrive at your destination.
How to Calculate Velocity
Examples
Average and Instantaneous Velocity
Speed vs. Velocity
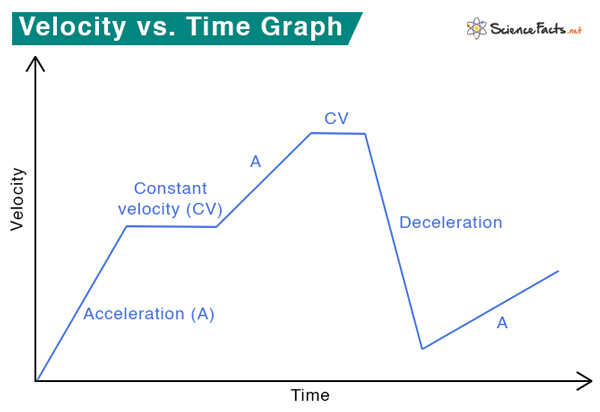
Velocity vs. Time Graph
Solved Problems
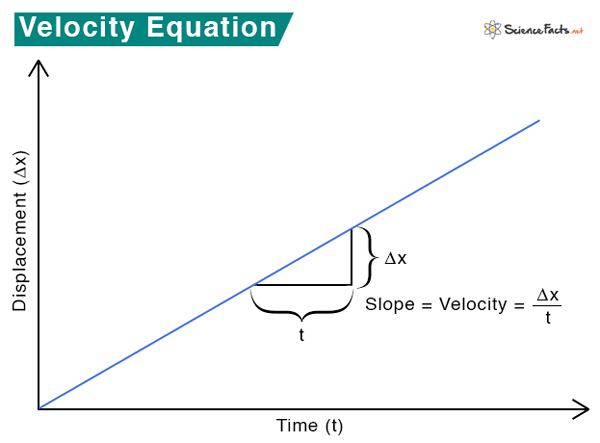
Velocity can be calculated by measuring the object’s displacement over the time taken to displace it. In vectorial notation, velocity is given by Units The SI unit of velocity is Newtons per second of N/s. The cgs unit is ergs per second or ergs/s. Other units include miler per hour or mph, kilometers per hour or kph, and feet per second or fps. Where, vavg is the average velocity xf is the final velocity xi is the initial velocity tf is the final time ti is the initial time If the starting time is zero, then ti = 0. The instantaneous (vins.) velocity is the velocity at a particular instant of time. It can be obtained by taking the limit of the above expression in the limit Δt → 0. Let us take an example to illustrate this. When we say a car is moving on the road at 35 mph, we specify the magnitude but not the direction. However, when we say a car is moving on the road eastwards at 35 mph, we specify both the magnitude and direction. The first sentence refers to the speed, and the second refers to the velocity. Therefore, speed is a scalar quantity, and velocity is a vector quantity. The formula for speed is the distance traveled over the time taken to travel that distance. Solution Given x1 = 75 m, x2 = 35 m, Δt = 5 s The average velocity is given by vavg = (x2 – x1)/Δt = (35 m – 75 m)/5s = – 8 m/s Therefore, the runner is running in the negative x-direction. Problem 2. A commuter train travels from New York to Philadelphia in 1 hour and 25 minutes and from Philadelphia to New York in 1 hour and 35 minutes. The distance between the two stations is approximately 96 miles. What is (a) the average velocity of the train and (b) the average speed of the train in m/s? (1 mile = 1.6 km) Solution a) The average velocity of the train is zero since the displacement is zero. (The train returns to New York). b) Given d = 96 miles = 96 x 1.6 = 153.6 km = 153.6 x 103 m t1 = 1 hr 25 mins = 60 mins + 25 mins = 85 mins = 85 x 60 = 5100 s Therefore, v1 = 153.6 x 103 m / 5100 s = 30.2 m/s t2 = 1 hr 35 mins = 60 mins + 35 mins = 95 mins = 95 x 60 = 5700 s Therefore, v2 = 153.6 x 103 m / 5700 s = 26.9 m/s The average speed is (30.2 m/s + 26.9 m/s)/2 = 28.55 m/s