[v_{T} = \sqrt{\frac{2mg}{C\rho_{air} A}} ] From this equation, one can see that the terminal velocity depends on:
Density of air, ρairMass of the object, mArea A of the object that is projected vertically. In other words, the object’s orientation.Drag coefficient C, which depends on the shape of the object
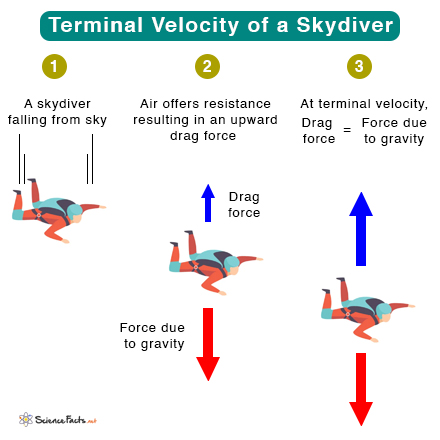
Thus, the speed achieved by a human during a free fall depends upon two factors – mass and orientation. Based on this, let us calculate the terminal velocity for two different positions.
1. Belly-down Position
2. Head Down Position
How can the Terminal Velocity be Increased
Given m = 75 kg ρair = 1.29 kg/m3 C = 1 A = 0.7 m2 g = 9.81 m/s2 Therefore, the terminal velocity is given by For the head-down dive, the drag coefficient is 0.7 and the projection area is 0.18 m2. Therefore, the terminal velocity comes out to be This is typically the fastest a human can skydive. However, the drag can be further minimized by streamlining the body such that a speed up to 310 mph can be reached.
being heavierdiving in thin, low-density airreducing the projected area by diving head firstreducing the drag coefficient by diving head firstwearing clothing to improve streamlining and reduce drag