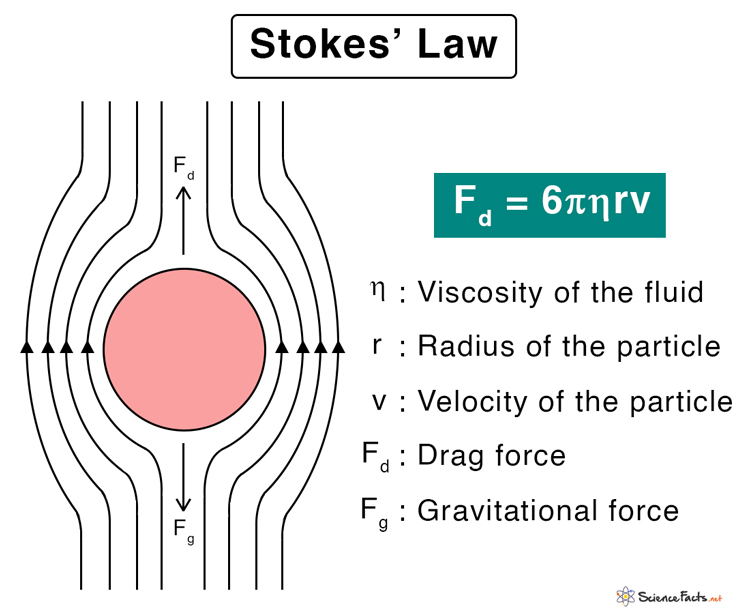
Historically, Stokes’ law has been named after Anglo-Irish physicist and mathematician George Gabriel Stokes after he derived the expression for drag force in 1851.
Stokes’ Law Equation
Assumption of Stokes’ Law
Derivation of Stokes’ Law
Stokes’ Law and Settling Velocity
Applications of Stokes’ Law
Limitations of Stokes’ Law
Fd = 6πηrv Where, η is the viscosity of the fluid r is the radius of the particle v is the velocity of the particle relative to the fluid SI Unit: Newton or N
Particles must be solid, smooth, and spherical.Particles must be of uniform density.Particles must be sufficiently large (>0.001mm) as compared to molecules of fluid so that the thermal (Brownian) motion of the fluid molecules does not affect the particles.Particles should not interfere with each other during the fall.The suspension should not have any turbulence, i.e., the flow must be laminar.
The radius of the sphere, rThe viscosity of the fluid, ηThe velocity of the particle, v
This proportionality can be represented as, Fd ∝ ηa rb vc Replacing the proportionality sign with the equality sign, Fd = k ηa rb vc Where k is the dimensionless proportionality constant Writing the above equation in terms of dimensions, [MLT-2] = [ML-1T-1]a [L]b [LT-1]c Or, [MLT-2] = Ma L-a+b+c T-a-c Equating the superscripts of mass, length, and time on both sides. 1 = a 1 = – a + b + c – 2 = – a – c Solving the above set of equations. a = 1 b = 1 c = 1 Therefore, Fd = k η r v Experimentally, the value of k was found to be 6π. Hence, Fd = 6πηrv By using the drag, buoyant, and gravitational forces, the particle’s terminal velocity is given by the following equation, where, r is the radius of the particle ρs is the density of the particle ρf is the density of the fluid Sedimentation is the propensity for particles in suspension to settle out of the fluid as deposits known as sediments. Stokes’ law is essential in understanding the sedimentation of small particles under the force of gravity. It can determine the sedimentation rate, which is the sediment’s terminal velocity. Stokes’ law can explain the floatation of clouds. Since raindrops are smaller in size, their terminal velocities are small. Therefore, they remain suspended in the air in the form of clouds. As they increase their size, their terminal velocities increase, and they start falling in the form of rain. When jumping off a plane, a parachute helps a person to slow down and land softly. The reason is that the person with the parachute achieves a terminal velocity. In Millikan’s oil drop experiment, Stokes’ law is used to determine the electron’s charge.