Standing Wave Animation
Image Courtesy: Physicsclassroom.com
Two people shaking either end of a jump ropeOcean or pool waves hitting a wall and bouncing back in the opposite directionPlucking the strings of a guitar. A guitarist can purposely alter the pitch of the sound by placing a finger on the string to shorten the length that is vibrating.Wind instruments that have air columns in them. The effective length of the tube determines the sound the pipe makes.In plates, rods, and diaphragms that are parts of percussion instruments and form an essential feature in many musical instrumentsIn optical media, such as optical cavities and waveguides.
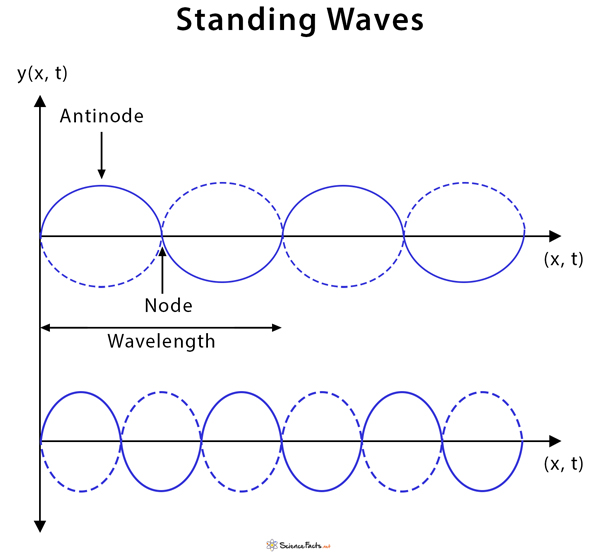
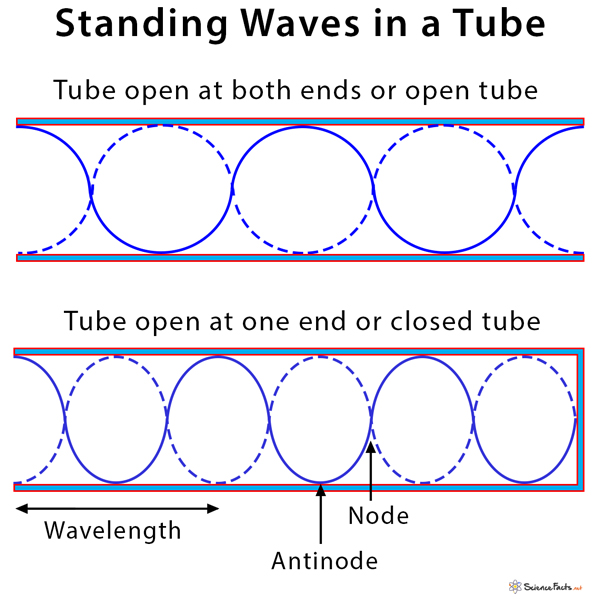
There is always energy associated with standing waves. This energy travels through a medium as a transverse pulse. Antinodes: Points on a standing wave where the wave vibrates with maximum amplitude due to constructive interference. Fundamental frequency: Lowest frequency of a standing wave that has the fewest number of nodes and antinodes. Harmonics: Higher frequencies that are integral multiples of the fundamental frequency. y1 = (A/2) sin (kx – ωt) y2 = (A/2) sin (kx + ωt) where the first wave is moving toward the right (positive x), and the second wave is moving toward the left (negative x). The factor of 1/2 is placed for convenience. Adding these two waves gives the total displacement at any point and time: yT = y1 + y2 = (A/2) sin (kx – ωt) + (A/2) sin (kx + ωt) = (A/2)[sin (kx – ωt) + sin (kx + ωt)] Recall that, Sin (A+B) = sin A cos B + cos A sinB Sin (A-B) = sin A cos B – cos A sin B Therefore, Sin (A-B) + Sin (A+B) = 2 sin A cos B Hence, yT = (A/2) 2sin (kx) cos (ωt) Or, yT = sin (kx) cos (ωt) In the boldface equation above, the displacement varies with distance as sin kx, but changing the time does not shift the location of peaks and troughs. It merely changes the amplitude. For example, at x=0, the displacement is always zero, no matter what the value of t. Hence, the velocity of a standing wave is zero. The length of a tube determines the frequency of a standing wave in the tube. Several complications arise depending on if one or both ends are closed or open. If an end is open, the air can move freely, and so there is maximum air movement or a displacement antinode at that end. An open tube or pipe is defined as one that is open at both ends. For such a tube, a standing wave can form if the wavelength of sound results in antinodes at both ends. Many musical instruments are made of a tube that is closed at one end but opened at the other. Such an instrument is known as a closed tube or pipe. Like an open tube, they can form a standing wave with the sound of an appropriate frequency. In this case, the resultant wave pattern forms an antinode at the open end and a node at the closed end.