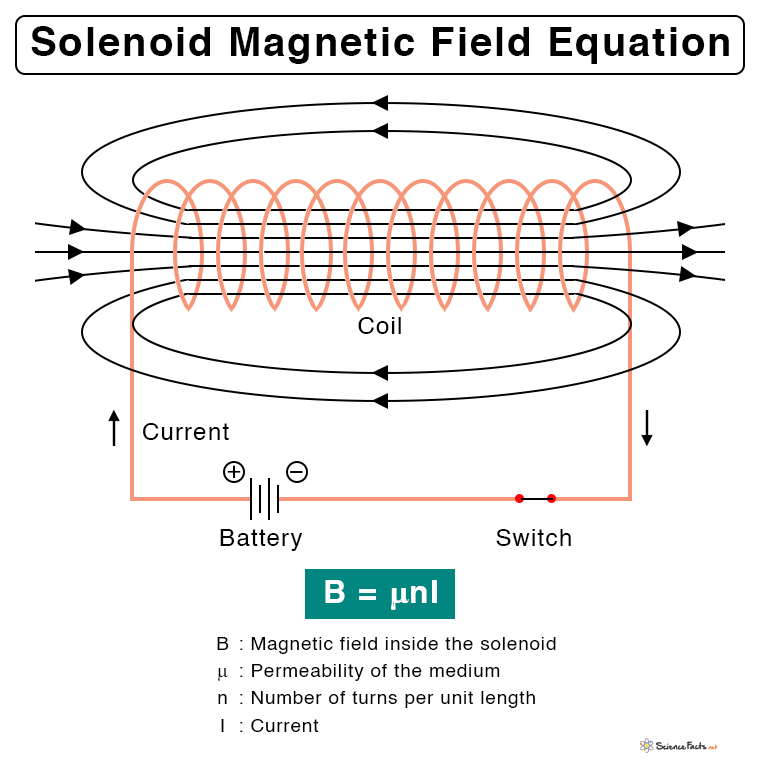
A solenoid can be used as an electromagnet when the ends are connected to a battery. A current passing through it induces a controlled magnetic field whose direction is given by the right-hand rule. The magnetic field can be enhanced by wrapping the wire around a solid metallic core, typically iron, forming a medium for the field to flow. However, the loops of wire are kept insulated from one another.
Solenoid Magnetic Field Equation
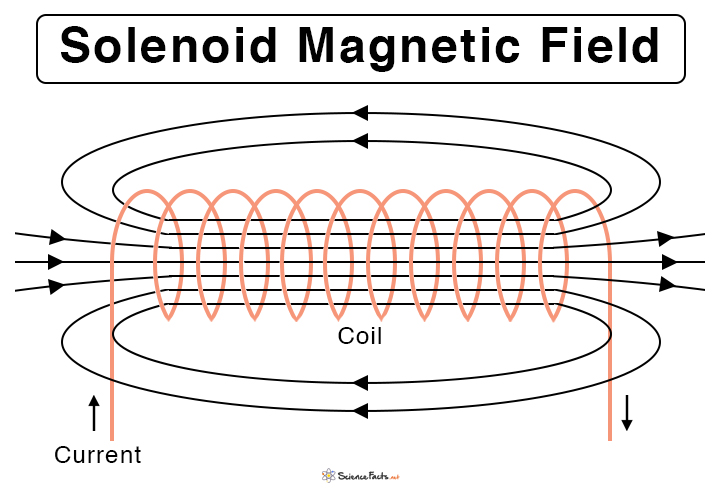
Direction of Magnet Field Lines
Where To calculate the magnetic field, we imagine a circle that encloses the current. Then, take the dot product of the magnetic field and an infinitesimal length of the circle and integrate it over the entire circle. Magnetic Field Inside the Solenoid The magnetic field inside a solenoid is given by, Where, n: Number of turns of the coil per unit length or turn density I: Current passing through the solenoid μ: Permeability of the metallic core If the core is hollow, then the medium is absent. The equation is given by, Where, μo: Permeability of air or vacuum Here, n is the number of turns of the coil per unit length of the solenoid. The above equation is suitable for an infinitely long solenoid. For a solenoid of finite length, the equation can be written as, Where, N: Total number of turns of the solenoid L: Length of the solenoid n = N/L: Density of turns From the above equations, it can be seen that the magnetic field inside a solenoid is,
Proportional to the number of turns or turn densityProportional to the currentDoes not depend on the distance from the axis
The magnetic field inside the solenoid remains constant and does not depend on the position. Therefore, the magnetic field is uniform throughout the inside of the solenoid. The small magnetic fields caused by the current in each turn of the coil add together to make a strong field. The presence of ferromagnetic material like iron, with high permeability, increases the field strength. Magnetic Field Outside the Solenoid The magnetic field lines exist outside the solenoid. However, they are not as dense as inside. Therefore, the flux density is much lower. Since the magnetic flux density measures the strength of the magnetic field, the field outside is negligible or zero. Using Ampere’s law to derive the magnetic field will yield the same result. The magnetic lines of force are also analogous to that of a bar magnet. They are straight and parallel and follow a longitudinal path inside the solenoid. Outside, the lines diverge and flow in the opposite direction to inside and complete the loop.