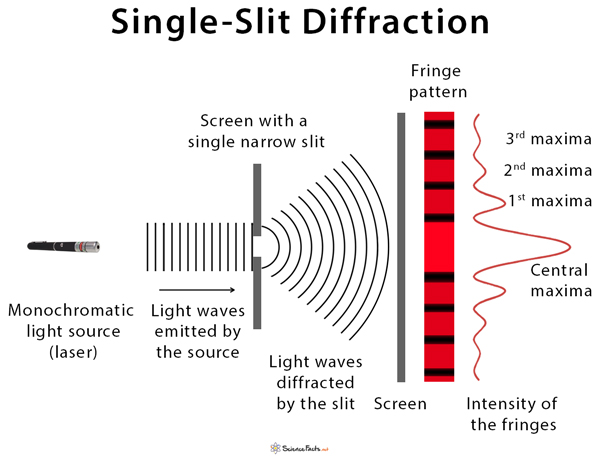
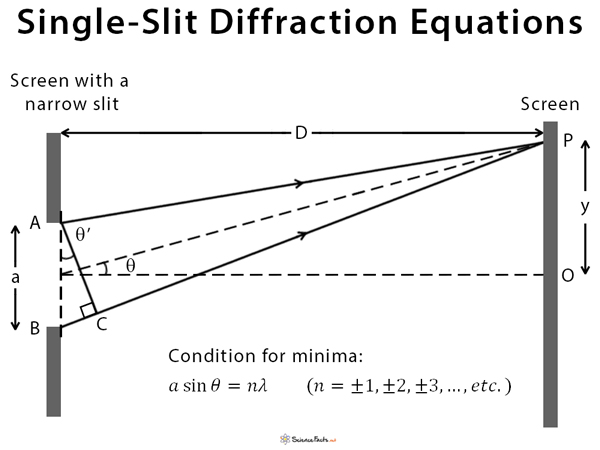
Huygens’ Principle
According to Huygens’ principle, every unobstructed point on a wavefront will act as a source of secondary spherical waves. The new wavefront is the surface tangent to all the secondary spherical waves. Therefore, each part of the slit can be thought of as an emitter of waves. We assume that the screen is at a considerable distance from the slit, i.e., D » a. Hence, θ = θ’ And, sin θ ≈ tan θ ≈ θ = y/D The path difference between the two rays AP and BP is given by, Δ = BP – AP = BC In the right-angled triangle BCA, sin θ’ = sin θ = BC/BA BC = BA sin θ = a sin θ Therefore, Δ = a sin θ Diffraction Minima The condition for minima or dark fringe is, Path difference = integral multiple of wavelength or, Δ = nλ (n=±1, ±2, ±3, … , etc.) or, a sin θ = nλ or, ay/D = nλ or, yn = nλD/a This equation gives the distance of the n-th dark fringe from the center. The fringe width is given by, β = yn+1 – yn = (n+1)λD/a – nλD/a or, β = λD/a Diffraction Maxima The condition for maxima or bright fringe is, Path difference = non-integral multiple of wavelength or, Δ = (n+1/2)λ (n=±1, ±2, ±3, … , etc.) or, a sin θ = (n+1/2)λ or, ay/D = (n+1/2)λ or, yn = (n+1/2)λD/a The intensity of single-slit diffraction is given by, I = I0 [sin (π a sin θ/λ)/( π a sin θ/λ)]2