Understanding rotational kinetic energy allows us to analyze spinning tops, rotating wheels, and celestial bodies like planets. It also has practical applications in engineering fields like mechanics and robotics.
Formula
Examples
Applications
Solved Problems
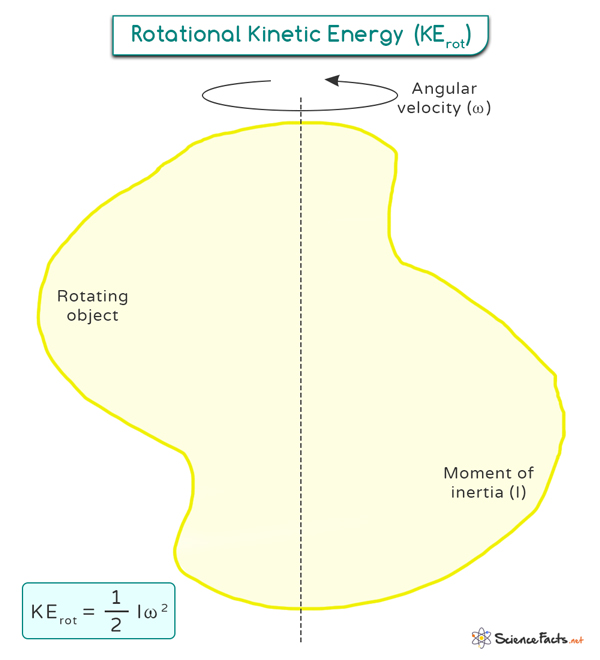
How fast the object is spinningHow much mass the spinning object hasWhere the mass is located compared to the spin
The formula for rotational kinetic energy is given by: KErot = ½ Iω2 where KErot is the rotational kinetic energy I is the moment of inertia ω is the angular velocity This formula shows that the rotational kinetic energy is directly proportional to the square of the angular velocity and the object’s moment of inertia. Angular velocity represents how quickly an object is rotating. The moment of inertia depends on both the mass and distribution of mass within the object. Objects with more mass concentrated farther from the axis of rotation have higher moments of inertia, resulting in higher rotational kinetic energy for a given angular velocity. Unit and Dimension The SI unit of rotational kinetic energy is Joule (J), which is equivalent to kg m²/s². This unit is derived from the formula for rotational kinetic energy, where the moment of inertia is expressed in kg m² and angular velocity in rad/s. It is important to note that this unit aligns with the fundamental principles of energy and motion in the metric system. The dimensional formula is [M1L2T-2].
1. Rolling Solid Sphere
Imagine a solid sphere rolling down a hill. As the sphere descends, it possesses both translational and rotational motion. The sphere’s rotation around its axis contributes to its rotational kinetic energy. The translational and rotational kinetic energies determine the sphere’s overall energy as it moves downhill.
2. Rotating Cylinder
Visualize a cylindrical object, like a can, spinning around a fixed axis. The rotation of the cylinder gives rise to its rotational kinetic energy. The moment of inertia of the cylinder plays a significant role in determining how much energy is stored in its rotation. The greater the moment of inertia and the faster the cylinder spins, the more rotational kinetic energy it possesses. This principle applies to a wide range of rotating objects, from wheels to cylinders used in machinery.
3. Spinning Top
A spinning top is a classic example of an object exhibiting rotational kinetic energy. As the top spins around its central axis, it possesses energy due to its angular velocity and moment of inertia. The top’s ability to remain upright while spinning results from the conservation of angular momentum, a concept closely related to rotational dynamics. The interplay between its motion and the stored rotational energy enables the top to exhibit its fascinating spinning behavior.
4. Rotating Wind Turbine
The rotating blades of a wind turbine exemplify the conversion of wind energy into rotational kinetic energy. As the wind pushes against the blades, they rotate around their axis. This rotational motion is then transformed into electrical energy through generators. The design of wind turbines takes into account factors such as blade shape, size, and wind speed to optimize the extraction of rotational kinetic energy from the wind.
5. Planet
On a cosmic scale, the rotation of planets is governed by rotational kinetic energy. Planets like Earth rotate on their axes, alternating between day and night. The rotation of a planet involves a massive amount of energy due to its substantial moment of inertia and relatively slow rotation rate. This rotational kinetic energy contributes to phenomena like the Coriolis effect, which influences atmospheric and oceanic currents and shapes planetary features over geological timescales. Solution Given I = 0.1 kg m² and ω = 5 rad/s The rotational kinetic energy is: KErot = ½ × 0.1 × (5)2 = 1.25 J Problem 2: Determine the rotational kinetic energy of a planet rotating at 1 × 10-4 rad/s with a moment of inertia of 8 × 1034 kg m². Solution Given I = 8 × 1034 kg m² and ω = 1 × 10-4 rad/s The rotational kinetic energy is: KErot = ½ × 8 × 1034 × (1 × 10-4)2 = 4 × 10-25 J Problem 3: Suppose a solid sphere with a mass of 2 kg and a radius of 0.5 m rotates at an angular velocity of 4 rad/s. What is its rotational kinetic energy? Solution Given M = 2 kg, R = 0.5 m, and ω = 4 rad/s The moment of inertia of a solid sphere is (2/5)MR2. I = (2/5)MR2 = (2/5) × 2 × (0.5)2 = 0.2 kg m² The rotational kinetic energy is: KErot = (1/2) × 0.2 × (4)2 = 1.6 J Problem 4: Suppose we have a solid cylinder with a mass of 4 kg and a radius of 0.3 m, rotating at an angular velocity of 6 rad/s. What is its rotational kinetic energy? Solution Given M = 4 kg, R = 0.3 m, and ω = 6 rad/s The moment of inertia of a solid cylinder is (1/2)MR2. I = (1/2)MR2 = (1/2) × 4 × (0.3)2 = 0.18 kg m² The rotational kinetic energy is: KErot = (1/2) × 0.18 × (6)2 = 1.6 J = 3.24 J