Reynolds number is named after British physicists Osborne Reynolds, who popularized its use in 1883.
Equation
Critical Reynolds Number
Example Problems and Solutions
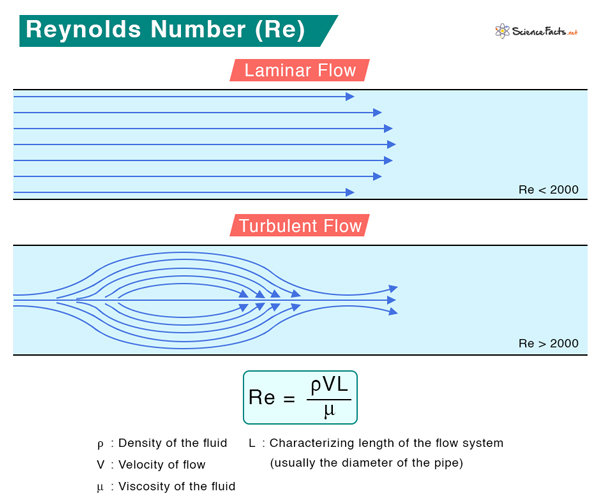
Where ρ is the density of the fluid V is the velocity of the flow L is the characterizing length in the flow system (usually the diameter of the pipe) μ is the viscosity of the fluid The number helps to categorize laminar flow from turbulent flow of any fluid like air or water. Laminar flow refers to the smooth and steady flow. It is also known as streamline flow. On the other hand, turbulent flow is irregular and chaotic due to the fluid’s changing velocity. If Re < 2000, the flow is laminar. If Re > 2000, the flow is turbulent. Unit and Dimension Reynolds number is a dimensionless quantity and does not have any unit. We can prove it by taking the division of inertial force and viscous force dimensions. Solution Given ρ = 80 kgˑm-3 V = 6 mˑs-1 L = 0.25 m μ = 0.7 Nˑsˑm-2 = 0.7 kgˑmˑs-2ˑsˑm-2 = 0.7 kgˑm-1ˑs-1 The Reynolds Number is Re = ρVL/μ => Re = (80 kgˑm-3 x 6 mˑs-1 x 0.25 m)/0.7 kgˑm-1ˑs-1 => Re = 120 kgˑm-1ˑs-1ˑ/0.7 kgˑm-1ˑs-1 => Re = 171 Since Re < 2000, the flow is Laminar.