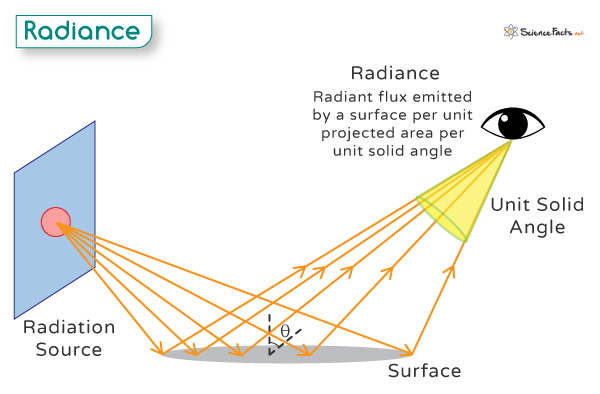
Simply put, radiance measures how much light comes from a specific area in a specific direction. It tells us how intense the light is when we look at a tiny piece of a surface from a particular angle. For example, when you hold a leaf, the amount of sunlight (brightness) you see coming through the leaf in a specific direction is like measuring the radiance.
Formula
Units
Applications
Example Problems with Solutions
The formula for radiance is given by: Where: – L is the radiance – φ is the radiant flux – A is the area of the source – ω is the solid angle – θ is the angle between the surface normal and the radiance direction This formula accounts for the fact that radiance varies with the angle of observation, with the cosine term (cos θ) representing the geometric relationship between the surface normal and the direction of observation. Solution: Given:
Radiant flux: φ= 500 WSurface area: A = 2 m²Solid angle: ω = π srcos θ = 1/π
Therefore, L=5002 ⋅π⋅1πL=500W/m²2m²⋅π⋅1π =>L=5002=250W/(m²⋅sr)=>L=5002=250W/(m²⋅steradian) The radiance is 250 W/m2 ∙ sr Problem 2: A surface has a radiance of 150 W/(m²·sr) with a solid angle of 0.5 steradian and a surface area of 3 m². Calculate the radiant flux. Assume cos θ = 1/π. Solution: L=ΦA⋅ω⋅cos(θ)L=dΦdA⋅dω⋅cos(θ) Rearranging the formula to solve for radiant flux:
Given:
Radiance: L = 150 W/(m²·sr)Solid angle: ω = 0.5 steradianSurface area A = 3 m²cos θ = 1/π
The radian flux is 71.65 W