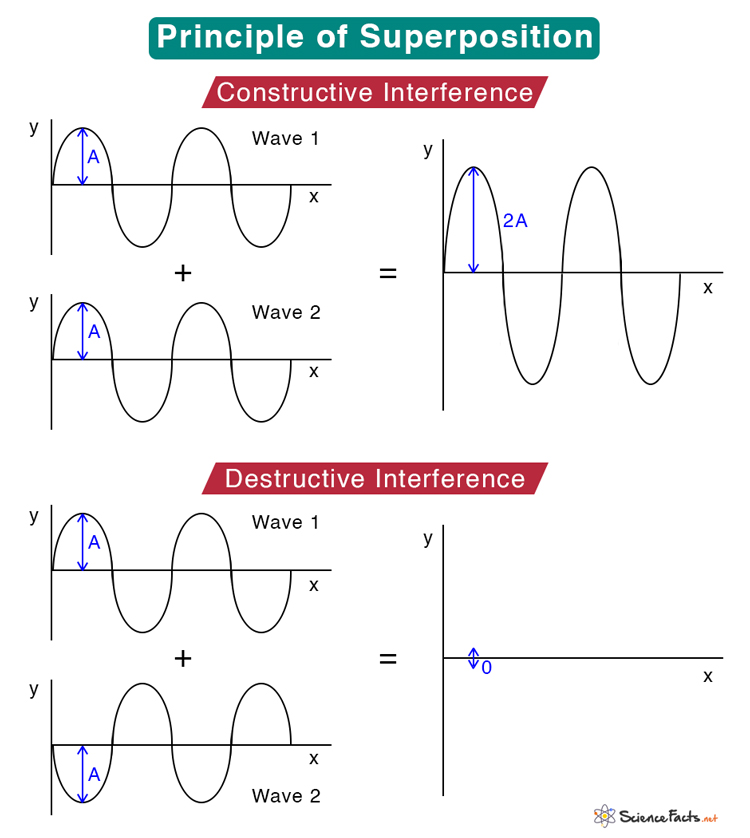
Superposition is an important concept as it can explain many phenomena in physics. The interference and diffraction of waves and standing waves are based on the superposition principle. This principle holds for all kinds of waves, like sound waves, light waves, electromagnetic waves, and surface waves.
Superposition Principle and Interference of Waves
Superposition Principle Equations
Example Problems
F (x1 + x2) = F (x1) + F (x2) Consider two waves whose displacements are given by y1 and y2. Then, according to the principle of superposition, the net displacement y is given by y = y1 + y2 The above equation can be generalized to n number of waves whose displacements are y1, y2, y3,…,yn. In such case, the net displacement is given by y = y1 + y2 + y3 + … + yn For the above equation to be valid, y1, y2, y3, …, yn must be linear. Suppose the displacement is a function of the position x. Then, y is written as y ≡ y (x). The superposition of the two functions y1 (x) and y2 (x) is given by y (x) = y1 (x) + y2 (x) Consider a wave traveling along a stretched string with amplitude A, frequency ω, and wave number k. Its time-dependent displacement is given by y1 (x, t) = A sin (kω – t) Another wave traverses along the string but is shifted by a phase ø. Its displacement is given by y2 (x, t) = A sin (kω – t + ø) The two waves are coherent. Let us apply the superposition principle to combine these two waves and obtain the net displacement. y (x, t) = y1 (x, t) + y2 (x, t) => y (x, t) = A [sin (kω – t) + sin (kω – t + ø)] => y (x, t) = 2A cos (ø/2) · sin (kω – t + ø/2) Like its constituents, the resultant wave is sinusoidal, traveling in the positive x-direction with an amplitude 2A cos (ø/2). Its phase angle is half the phase difference of its constituent waves. Solution Given y1(t) = 5 sin(ωt) and y2(t) = 2 sin (ωt + π/2) = 2 cos (wt) The resultant displacement is y(t) = y1(t) + y2(t) => y(t) = 5 sin(ωt) + 2 cos (wt) The resultant amplitude is A = √(52 + 22) = 5.39