Symbol: P.E., U, or V SI Unit: Joule or J (1 J = 1 kg m2/s2) Cgs Unit: erg (107 erg = 1 J) Dimensions: [M L2 T-2] When was Potential Energy Discovered Scottish engineer William Rankine coined the term potential energy in 1853.
Types of Potential Energy
Change in Potential Energy
Solved Problems
1. Gravitational Potential Energy
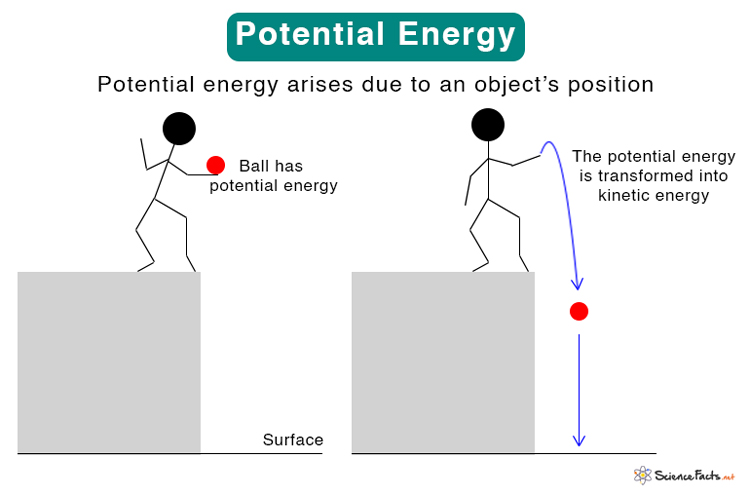
The gravitational potential energy is due to the Earth’s gravitational force. It is the energy stored in an object due to its height from the surface of the Earth.
Examples
Here are some examples of gravitational potential energy found in the home, everyday life, and nature.
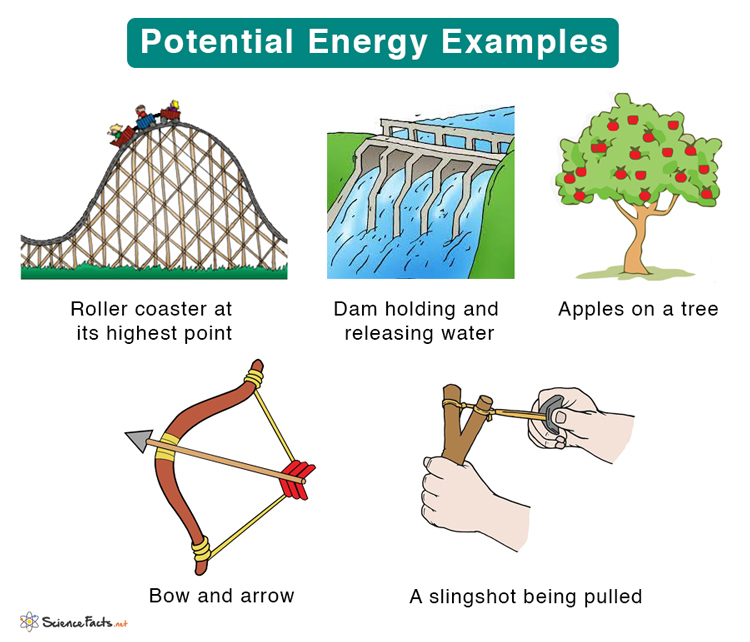
A cart on the top of a hillA roller coaster resting on its highest pointA child at the top of a slideWater stored in an overhead tankA yoyo before being releasedA pendulum at its extreme position
Equation
The gravitational potential energy depends on two factors – the object’s mass and its height from Earth’s surface. Suppose an object of mass m is at a height h from the surface of the Earth. Then, the potential energy can be calculated from the following equation. P.E. = mgh Where m: mass of the object h: height of the object from Earth’s surface g: acceleration due to gravity (= 9.81 m/s2) From the above equation, it is clear that the more massive an object is, the greater is its potential energy. Also, the potential energy increases as the height increases. When the object is released, it accelerates downwards due to gravity. It means that gravity does work on the object to move it downwards. Since its height decreases, it loses potential energy. From the law of energy conservation, the loss in potential energy is equal to the gain in kinetic energy. When the object reaches the surface, h = 0, P.E. = 0. It means that the gravitational potential energy of an object on Earth’s surface is zero. The work done by gravity does not depend on the path taken. Hence, potential energy is conservative.
2. Elastic Potential Energy
The energy stored in an elastic material due to stretching or compressing is the elastic potential energy. When the stress is released, the potential energy is converted into kinetic energy or other forms like heat.
Examples
SpringRubber bandSlingshotTrampolineBungee cordCantileverBow and arrowBalloon
Equation
In order to understand the equation for elastic potential energy, let us take the example of a spring. Spring is a device that can store potential energy when stressed or compressed. Suppose a spring is compressed or extended by a distance x. Then, its elastic potential energy can be determined by the following equation. P.E. = ½ kx2 Where x: distance by which the spring is stretched or compressed k: spring constant When it is stretched or compressed, the spring stores potential energy. When it is released, the potential energy is converted to kinetic energy. The spring starts to oscillate about its equilibrium position (x = 0). The following image shows a few examples of gravitational and elastic potential energy.
3. Electric Potential Energy
The work done in moving an electric charge from one point to another in an electric field is called electric potential energy. The electric field can be generated by a point charge, conducting sphere, or capacitor. For example, a system of point charges has potential energy.
Equation
To understand the equation for electric potential energy, let us take the example of a parallel plate capacitor. Suppose a charge +q is placed inside a parallel plate capacitor, whose plates are separated by a distance d. Let E be the electric field of the capacitor. Then, the electric potential energy V can be calculated by the following equation. V = qEd Where q: point charge E: electric field d: distance of separation between the two plates of the capacitor The following image shows the equations for potential energy. Aside from the ones discussed above, three other types of potential energy are chemical potential energy, nuclear potential energy, and magnetic potential energy. ΔP.E. = (P.E.)final – (P.E.)initial Example: Gravitational Potential Energy When an object falls from a height h to ground, the change in potential is given by, ΔP.E. = (P.E.)final – (P.E.)initial Or, ΔP.E. = 0 – mgh Or, ΔP.E. = –mgh The negative sign implies that work is not done against the Earth’s gravitational force. When the same object is raised to a height h, the change in potential energy is given by, ΔP.E. = (P.E.)final – (P.E.)initial Or, ΔP.E. = mgh – 0 Or, ΔP.E. = mgh In this case, work is done to raise the object. Hence, the potential energy is positive. Thus, the change in potential energy is not always negative. Solution: Given, m = 5 kg, h = 8 m P.E. = mgh Or, P.E. = 5 kg x 9.81 km/s2 x 8 m Or, P.E. = 392.4 J Problem 2: A ball of mass 1.2 kg is pushed upward on an inclined plane. Calculate the potential energy gained by this ball, given that the height of the wedge is 1.2 meters. (g = 9.81 m/s2) Solution: Given, m = 1.2 kg, h = 1.2 m P.E. = mgh Or, P.E. = 1.2 kg x 9.8 m/s2 x 1.2 m Or, P.E. = 14.1 J Problem 3: A man climbs onto a wall of height 3.8 m and gains 2186 J of potential energy. What is the mass of the man? Solution: Given, h = 3.8 m, P.E. = 2186 J or kg m2/s2 We have, P.E. = mgh Or, m = P.E./gh Or, m = 2186 kg m2/s2/(9.81 m/s2 x 3.8 m) Or, m = 58.6 kg