Planck hypothesized that when an oscillator jumps from a higher energy state, E1, to a low energy state, E2, the difference in energy between the two states is proportional to the frequency ν at which the radiation is emitted. Mathematically, the following equation shows how much is one quantum of radiation. ΔE = E2 – E1 = hν Where h is called Planck’s constant, its value is 6.67 x 10-34 J s.
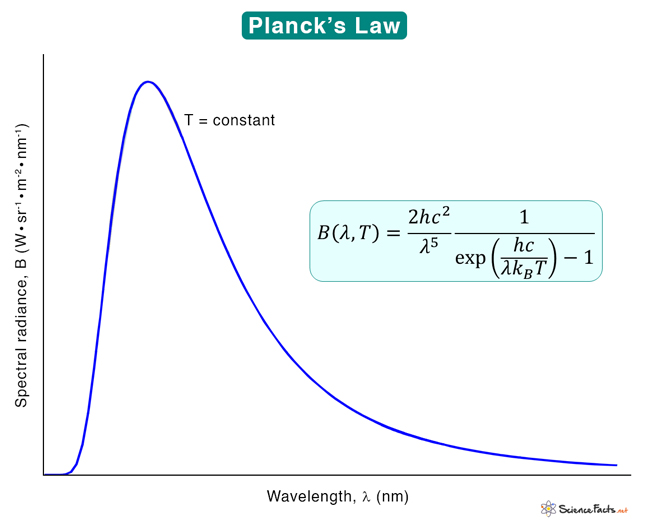
Planck’s Law Formula
Where B: Spectral radiance ν: Wavelength of radiation T: Absolute temperature c: Speed of light h: Planck’s constant The spectral radiance can also be measured per unit wavelength instead of unit frequency. In this case, the equation gets modified to: The SI unit of B(ν, T) is W·sr−1·m−2·Hz−1, and that of B(λ, T) is W·sr−1·m−3. In the low-frequency limit, Planck’s law approximates to Rayleigh-Jeans law. In the high-frequency limit, Planck’s law approximates Wien’s law. Planck’s law follows the distribution of energy according to Bose-Einstein statistics. The above expressions are obtained by multiplying the density of states in terms of frequency or wavelength with the photon energy and the Bose-Einstein distribution function with the normalization constant set to one.