Formula
Proof
Applications
Example Problems
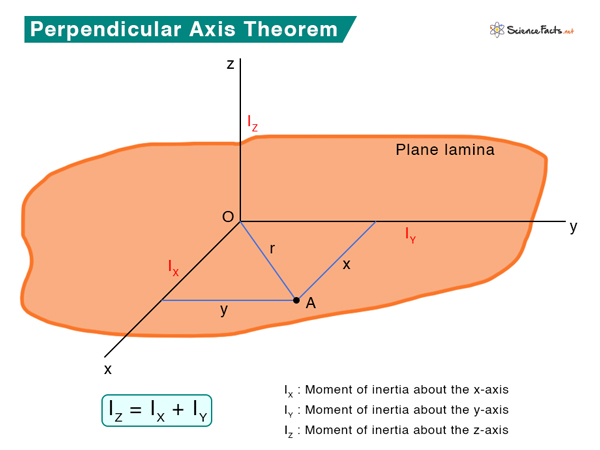
IZ = IX + IY Where IX, IY, and IZ are the moments of inertia about the x-, y-, and z-axis, respectively. The expressions for the moment of inertia about the three axes are given by Using Pythagoras’ theorem, r2 = x2 + y2 Therefore, IZ = (\int )(x2 + y2) dm => IZ = (\int )x2 dm + (\int )y2 dm => IZ = IX + IY Thus, we have proved the perpendicular axis theorem.
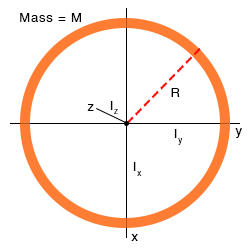
1. Ring
The moment of inertia of a ring of mass M and radius R about the z-axis is Due to the symmetry of the ring, IX = IY = I. Therefore,
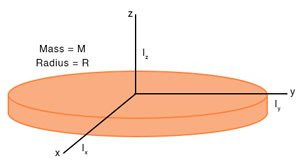
2. Disc
The moment of inertia of a disc of mass M and radius R about the z-axis is given by Due to the symmetry of the disc, IX = IY = I. Therefore,
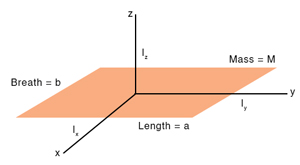
3. Rectangular Section
The moment of inertia of a rectangular section of mass M, length a, and breath b about an axis passing through its center and parallel to its length is Similarly, the moment of inertia about an axis passing through the center and parallel to the breath is Using the perpendicular axis theorem Solution Let the center of the rod be at the origin. Suppose the rod is in the XY plane and along the x-axis. Then, the z-axis is perpendicular to the rod, and the moment of inertia about the z-axis is IZ = ML2/12 Using the perpendicular axis theorem IZ = IX + IY Since the rod is thin, its rotation about its axis can be neglected; that is, IX = 0 Therefore, IZ = IY => IY = ML2/12 Problem 2. Suppose the rod in problem 1 has a mass of 1.5 kg and a length of 70 cm. What are the moments of inertia about the x, y, and z axes? Solution Given M = 1.5 kg and L = 70 cm = 0.7 m The moment of inertia values are IX = 0 IY = IZ = ML2/12 = (1.5 kg) (0.7 m)/12 = 0.735 kgˑm2