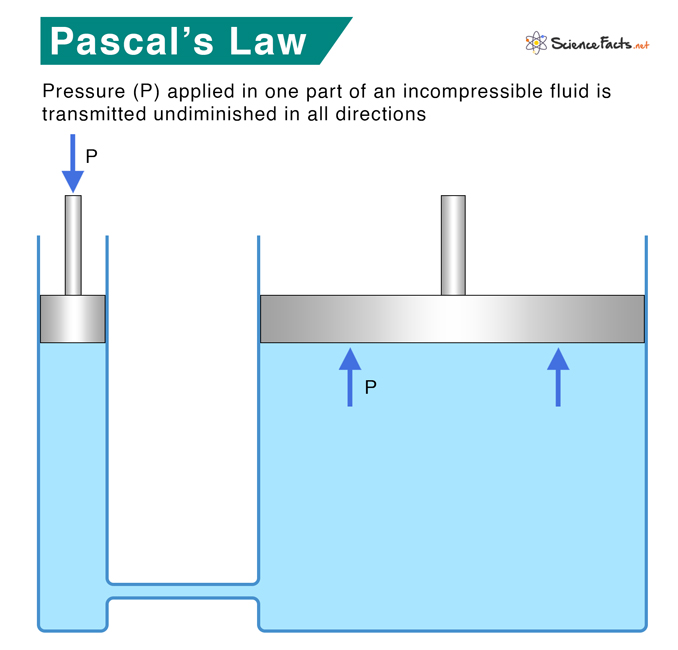
French mathematician Blaise Pascal established this law in 1653 and published it in 1663.
Explanation
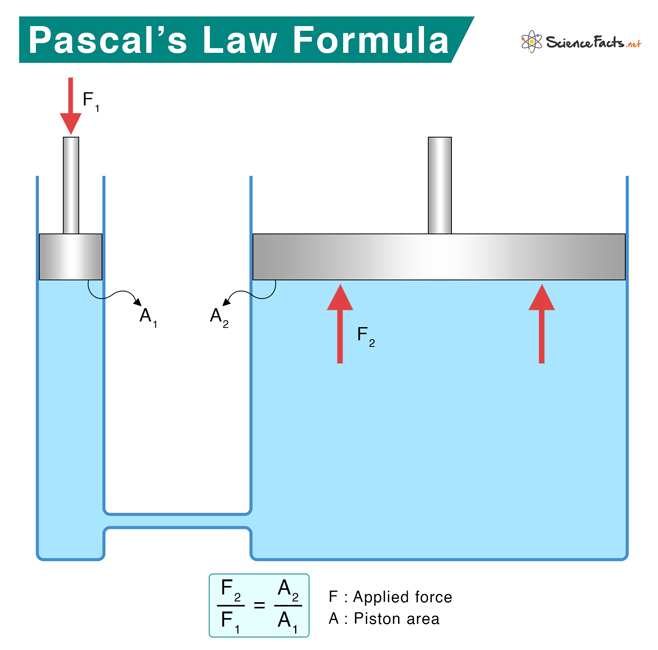
Formula for Pressure
Applications
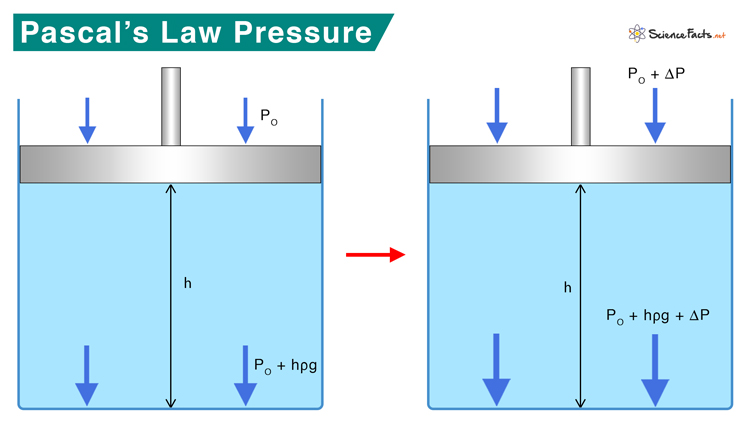
Ptop = Po Where, Ptop is the pressure at the top, and Po is the atmospheric pressure. The pressure at the bottom of the container is equal to the pressure at the top plus the water column’s height. Pbottom = Ptop + hρg Where, Pbottom is the pressure at the bottom, h is the height of the air column, ρ is the density, and g is the acceleration due to gravity. Suppose the pressure at the top changes by Δp such that the new pressure is given by P’top = Po + Δp Since the fluid is incompressible, its volume will not change. Then, the new pressure at the bottom is P’bottom = P’top + hρg => P’bottom = Ptop + Δp + hρg => P’bottom = Pbottom + Δp Therefore, the pressure change at the bottom is Δp, the same as at the top. It means that the added pressure is transmitted from top to bottom undiminished. P = F/A Where, F is the applied force, P is the hydraulic pressure, and A is the surface area of the piston. We shall apply this formula and Pascal’s principle to study hydraulic systems. Suppose a downward force F1 is applied to the left piston having an area A1. This force creates a pressure change transmitted to all parts of the enclosed fluid. This results in an upward force F2 on the right piston having an area A2. We have the following equations for pressures P1 and P2 on the left and the right pistons, respectively. P1 = F1/A1 and P2 = F2/A2 According to Pascal’s law, the pressure is transmitted undiminished throughout the fluid. It means that the pressures at the two pistons are equal. Therefore, P1 = P2 => F1/A1 = F2/A2 => F1/F2 = A2/A1 The above equation assumes that the pistons are at the same vertical height and that friction in the system is negligible. Rewriting the above equation as F2 = (A2/A1) F1 Since A2 > A1, F2 > F1. Therefore, the force is multiplied. Suppose we apply a force of 100 N on the left piston, and the right piston has five times more area than the left one. The force on the right piston is 500 N. Thus, we started with a force of 100 N and ended with a force of 500 N. We have multiplied the force by using a hydraulic system. We have seen how hydraulic systems utilize Pascal’s law to lift objects. They have many applications in day-to-day life. A hydraulic jack is used in automotive repair shops to lift vehicles weighing more than one ton. A car uses a hydraulic braking system that enables it to stop. Stepping on the brake pedal prevents the wheels from rolling further. An aircraft use hydraulics and pneumatics in its braking system, landing gear, and flap. Other applications of Pascal’s law include squeezing toothpaste, pressing olive and hazelnut oils, and calibrating pressure gauges. It is also applied to devices like a jackhammer and hydraulic pumps.