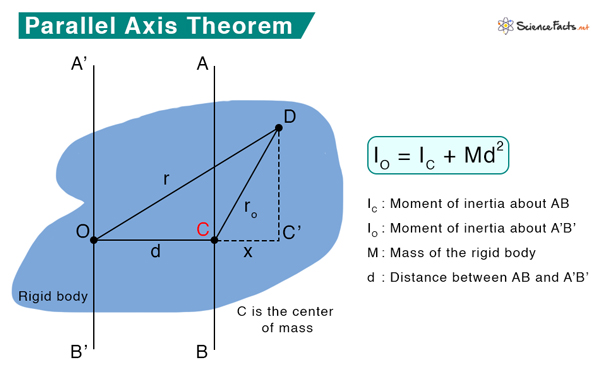
The parallel axis theorem is a convenient way to calculate the moment of inertia about any parallel axis since the moments of inertia few familiar objects can be found in tables.
Formula
Derivation
When to Use Parallel Axis Theorem
Example Problems
IO = IC + Md2 IC is the moment of inertia about an axis passing through the center of mass. IO is the moment of inertia about an arbitrary axis parallel to the axis passing through the center of mass. M is the object’s mass. d is the distance between the two parallel axes. We have the following quantities. M: Mass of the body dm: Infinitesimal mass of point D IC: Moment of inertia about AB IO: Moment of inertia about A’B’ h: Distance between the two parallel axes AB and A’B’ rₒ: Distance between points C and D r: Distance between points O and D x: Distance between points C and C’ The expressions for the moment of inertia are as follows: Consider triangle OC’D. (OD)2 = (OC’)2 + (C’D)2 => r2 = (d + x)2 + (C’D)2 => r2 = (d + x)2 + ro2 – x2 => r2 = d2 + x2 + 2dx + ro2 – x2 => r2 = ro2 + d2 + 2dx Multiplying both sides by dm and integrating The term ( \int x dm ) is zero since the integral of the moments of infinitesimal masses about the center of mass is always zero when the body is in equilibrium. Therefore, ( \int x dm = 0 ), and we get, IO = IC + Md2 Thus, we have derived the parallel axis theorem.
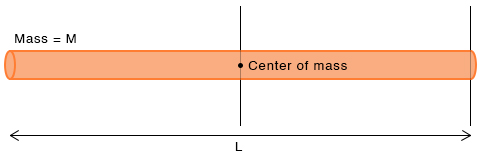
1. Uniform Rod
The moment of inertia IC of a thin rod of mass M and length L about an axis passing through its center is Let us apply the parallel axis theorem to find the moment of inertia about its edge IO. We know that the edge is at a distance L/2 from the center; d = L/2.
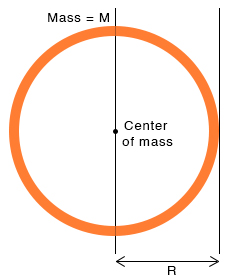
2. Ring
The moment of inertia IC of a ring of mass M and radius R about an axis passing through its center and perpendicular to the surface is IC = MR2 The edge is at a distance R from the center. Therefore, the moment of inertia about an axis tangential to the edge and perpendicular to the surface is IO = MR2 + MR2 => IO = 2MR2
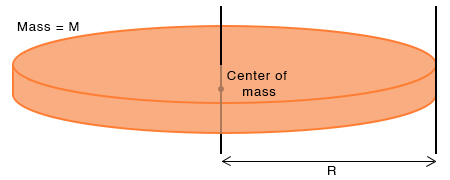
3. Disc
The moment of inertia IC of a disc of mass M and radius R about an axis passing through its center and perpendicular to the surface is The edge is at a distance R from the center. Therefore, the moment of inertia about an axis tangential to the edge and perpendicular to the surface is
4. Sphere
The moment of inertia IC of a solid sphere of mass M and radius R about its central axis is The surface is at a distance R from the center of the sphere. Therefore, the moment of inertia about an axis tangential to the surface is Solution Given IC = 35 kg m2, M = 55 kg, and d = 40 cm = 0.4 m From the parallel axis theorem, IO = IC + Md2 => IO = 35 kg m2 + 55 kg x (0.4 m)2 => IO = 43.8 kg m2 Problem 2. Find the moment of inertia of a uniform rod with IC = 0.06 kg m2, L = 0.3 m, and mass = 1.50 kg about an axis perpendicular to the rod and passing through a point at 1/8 of the length of the rod. Solution Given IC = 0.06 kg m2, L = 0.3 m, and mass = 1.50 kg From the parallel axis theorem IO = IC + Md2 Since the point is at a distance 1/8 of the length of the rod, we have d = L/2 – L/8 = (3/8) L => d = (3/8) x 0.3 m = 0.1125 m Therefore, the moment of inertia about an axis perpendicular to the rod and passing through the point in question is IO = 0.06 kg m2 + 1.50 kg x (0.1125 m)2 => IO = 0.079 kg m2