Examples
Simple Harmonic Motion
Damped Harmonic Motion
Oscillations of a pendulumVibration in a springMotion of a wheelMovement of a seesawVibrations in guitar stringsAlternating current in household equipmentElectromagnetic waves passing through the air
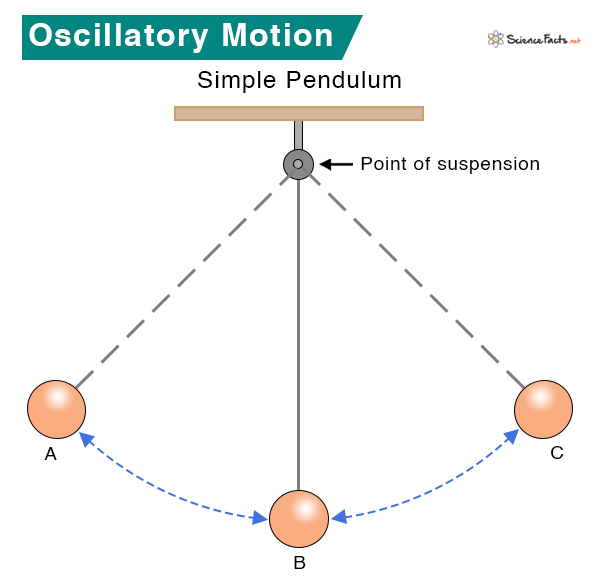
The example below shows a pendulum oscillating about its point of suspension. It passes through points A, B, and C during its oscillations.
Equation
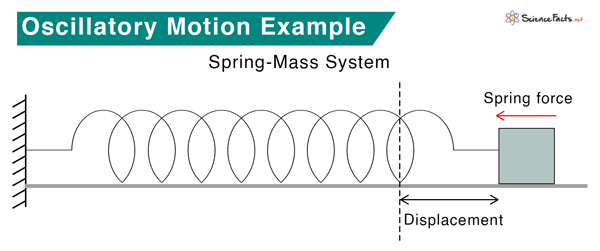
Consider a spring-mass system on a horizontal surface, as shown in the image. According to Hooke’s law, the restoring force on the oscillating object is proportional to its displacement. Where F is the restoring force x is the displacement k is the spring constant From Newton’s second law Where m is the mass of the object (\frac{d^2 x}{dt^2} ) is the acceleration expressed in differential form Comparing the two equations Where ( \omega = \sqrt{\frac{k}{m}} ) The above equation is a second-order linear differential equation whose solution is given by Where A is the amplitude ω is the angular frequency t is the time ø is the phase difference The constants A, ω, and ø can be determined by the boundary conditions of the system.
Equation
Consider the spring-mass system again, but it acts like a damped oscillator this time. The damping force is found to be proportional to the object’s velocity. The second-order differential equation modifies to Where b is an arbitrary constant. The term ( b \frac{dx}{dt} ) is the damping force. Rewriting the equation as Where ( 2\beta = \frac{b}{m} ) and ( \omega_o = \sqrt{\frac{k}{m}} ) The general solution of this equation is Where ( \omega_1 = \sqrt{\beta^2 – \omega_{o}^2} ) The exponential term in the expression is the decay function, and β is the damping coefficient. There are three types of damped oscillators:
under-damped, when β < ωoover-damped, when β > ωocritically damped, when β = ωo