The law is named after British mathematician Isaac Newton, who published it in 1701. Newton did not initially state his law in its current form. It was because of the confusion arising from the concept of heat and temperature, which did not exist during his time.
Mathematical Form of the Law
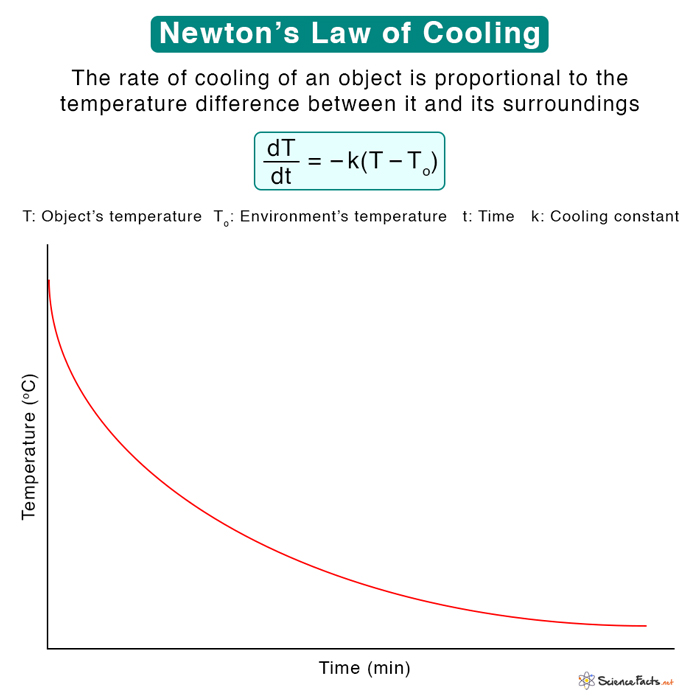
Newton’s Law of Cooling Formula
Limitations
Example Problems
where k is a positive constant known as the cooling constant. The negative sign implies that the object’s temperature is decreasing with time. Therefore, an object’s cooling rate depends on the following:
the temperature difference between it and its surroundingsthe cooling constant
From the above equation, we can make the following conclusions:
If the object is much hotter than its surroundings, T – To is large and has a high cooling rate. The object cools rapidly.If the object is slightly hotter than its surroundings, T – To is small, and the cooling rate is low. The object cools slowly.
It means a cup of hot coffee cools more rapidly when kept in the fridge than outside. Ti is the object’s initial temperature, and Tf is its final temperature. When t → ∞, Tf = To. The object attains the temperature of its surroundings eventually.
The temperature difference between the object and its surroundings must be low.Only heat lost by radiation is considered.The temperature of the surrounding must remain constant during the cooling process.
Solution. Given Ti = 70 oC, To = 25 oC, t = 5 mins, k = 0.051 min-1 We use the following equation. Tf = To + (Ti – To) e-kt => Tf = 25 + (70 – 25) exp (-0.051 x 5) = 59.9 oC Problem 2. A body with a temperature of 50 oC is kept in an environment of 25 oC. If the body’s temperature falls to 45 oC in 10 minutes, find out how much excess time it will take for the body to attain a temperature of 40 oC. Solution. Given Ti = 50 oC, Tf = 45 oC, To = 25 oC, t = 10 mins We use the following equation to find k. Tf = To + (Ti – To) e-kt => k = (1/t) ln[(Ti – To)/(Tf – To)] => k = (1/10 min) ln[(50 – 25)/(45 – 25)] = 0.051 min-1 For the second interval, Ti = 45 oC, Tf = 40 oC, k = 0.051 min-1 Therefore, additional time taken is t = (1/0.051 min-1) ln[(45 – 25)/(40 – 25)] = 5.64 min Problem 3. A body cools from 75 °C to 55 °C in 5 minutes. The temperature of its surroundings is 25 °C. What will be its temperature after the next 5 minutes? Solution. Given Ti = 75 oC, Tf = 55 oC, To = 25 oC, t = 5 mins We use the following equation. Tf = To + (Ti – To) e-kt => k = (1/t) ln[(Ti – To)/(Tf – To)] => k = (1/5 min) ln[(75 – 25)/(55 – 25)] = 0.102 min-1 For the second interval, Ti = 55 oC, t = 5 mins, k = 0.102 min-1 The final temperature is Tf = To + (Ti – To) e-kt => Tf = 25 + (55 – 25) exp(-0.102 x 5) = 43 oC