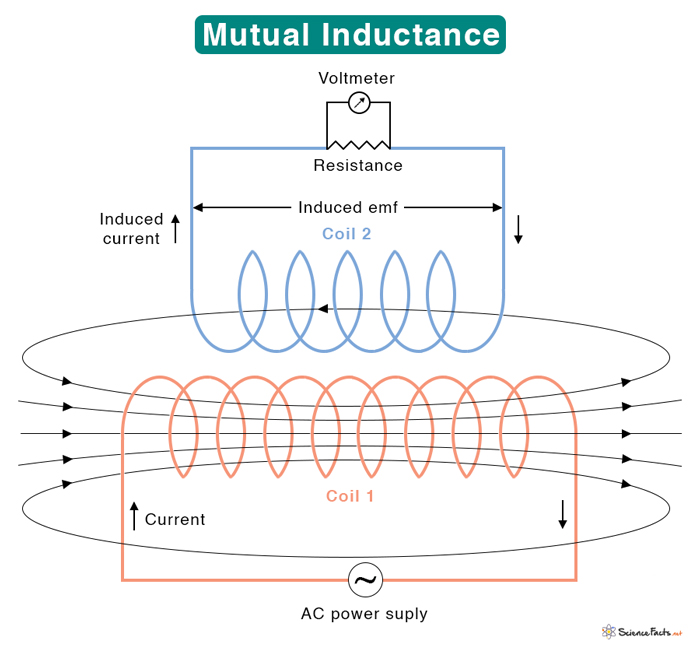
The induced emf will cause a current to flow in the second coil. Lenz’s law determines the direction of the induced current. This direction is such that it will oppose the change of current in the first coil. Now, suppose both the coils carry current. Then, emf will be induced in each coil due to changing current in the other. Hence, mutual inductance can also be defined as the property that describes the effect on one coil’s magnetic field with another coil’s magnetic field.
Mutual Inductance Equation
Applications of Mutual Inductance
Problems and Solutions
The rate of magnetic flux change in coil 2 is proportional to the rate of current change in coil 1. Therefore, The constant of proportionality M21 is the mutual inductance. It has the SI unit of Henry or H, named after American scientist Joseph Henry who discovered electromagnetic induction. 1 H = 1 Wb/A or 1 T·m2/A or 1 V·s/A. Rewriting the induced emf equation Thus, the mutual inductance can be defined as the ratio between the emf generated in coil 2 and the rate of current change in coil 1. It is also known as the coefficient of mutual induction. Now, consider the following equation again. The above equation is discrete in time. So, summing over all time increments we get This equation is used to calculate the mutual inductance between any two coils, as discussed below.
1. Mutual Inductance of Two Coils
Suppose two coils 1 & 2 with N1 and N2 turn have currents I1 and I2 flowing through them, as shown in the figure. The flux due to I1 and I2 are φ21 and φ12. The mutual inductance of coil 2 due to coil 1 is given by Similarly, the mutual inductance of coil 1 due to coil 2 is given by From the reciprocity theorem, the two mutual inductances are the same and can be represented by M. Therefore, The induced emfs in the two coils are given by Note that ε21 and ε12 do not represent the total emf in the circuit. Each coil can have its emf due to self-inductance. The mutual inductance depends upon how close the two coils are placed. If the coils are close enough, all the flux from coil 1 passes through coil 2. Then the mutual inductance is high. The mutual inductance is low if the coils are far. Also, the mutual inductance can be increased by increasing the number of turns of the coils or by enclosing the coils in a soft iron core. The advantage of having a soft iron core is that the magnetic flux leakage is reduced.
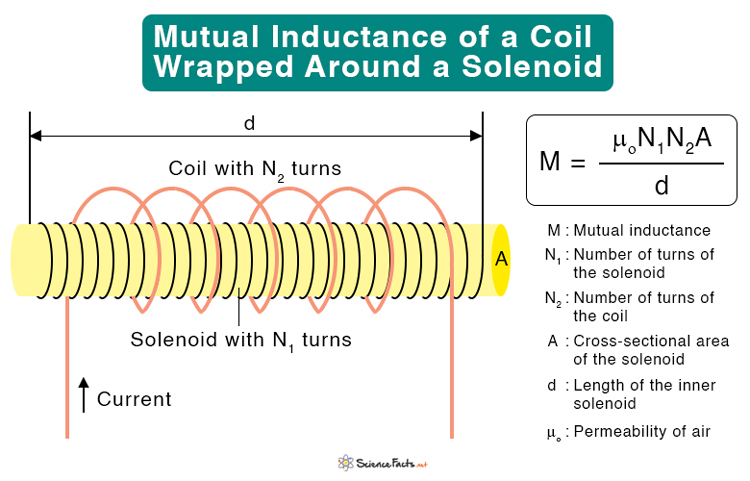
2. Mutual Inductance of a Coil Wrapped Around a Solenoid
Suppose a long solenoid with length d and cross-sectional area A consists of N1 turns of wire carries current I1, as shown in the figure. The magnetic field B inside a solenoid is given by Where μo (= 1.26 x 10-6 H/m) is called the permeability of air. A coil of N2 turns is wrapped around the solenoid such that the two are coaxial. The magnetic flux φ21 passing through each turn of the coil due to the solenoid is Thus, the mutual inductance is The self-inductance of a solenoid is Similarly, the self-inductance of the coil can be calculated and shown to be Multiplying L1 with L2, we get However, this equation assumes no flux leakage and perfect magnetic coupling between the two coils, L1 and L2. In reality, there is going to be some leakage due to alignment and the coupling can never be 100%. For this reason, we introduce a term calling coupling constant, k, such that the mutual inductance becomes k takes a value between 0 and 1. When k = 1, it means that all of the magnetic flux produced by the solenoid passes through the outer coil and vice versa.
TransformersGeneratorsMotorsMetal detectorsPacemakersRadio receivers
Solution: Given M = 4.75 × 10-4 H ΔI/Δt = 940 A/s The induced emf is given by |ε| = M ΔI/Δt = 4.75 × 10-4 H x 940 A/s = 0.45 V Problem 2: Calculate the mutual inductance between a solenoid of length 30 cm and cross-sectional area of 6.25 cm2 with 500 turns and a circular coil of 250 turns wound at the solenoid’s center (μo = 1.26 x 10-6 H/m). Solution: Given d = 30 cm = 0.3 m A = 6.25 cm2 = 6.25 x 10-4 m2 N1 = 500 N2 = 250 μo = 1.26 x 10-6 H/m The mutual inductance is given by M = μoN1N2A/d Or, M = 1.26 x 10-6 H/m x 500 x 250 x 6.25 x 10-4 m2/0.3 m Or, M = 0.000328 H or 3.28 x 10-4 H