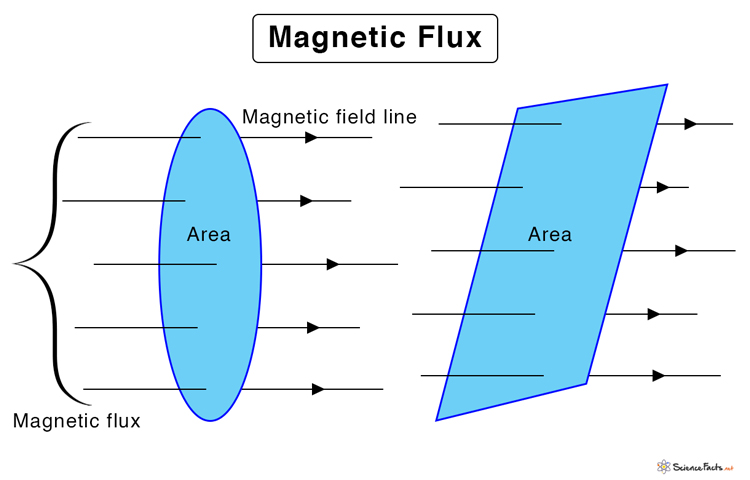
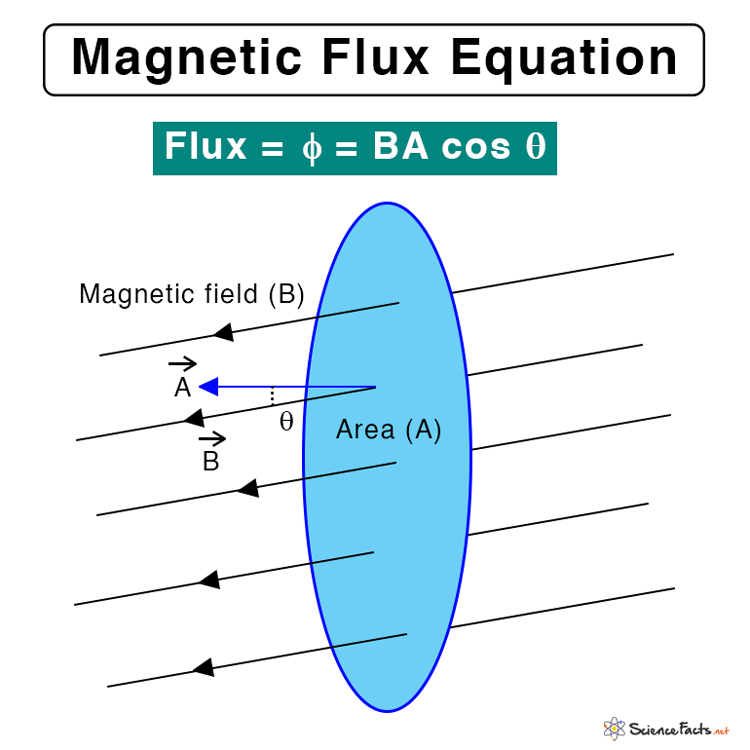
Magnetic Flux Equation
Significance of Magnetic Flux
Difference Between Electric Flux and Magnetic Flux
If the angle between the magnetic field vector and the area vector is θ, then the magnetic flux is given by Symbol: Greek letter phi, φ SI Unit: Weber or Wb CGS Unit: Maxwell Dimensions: [M1 L2 T-2 I-1] When θ = 0o , φ = BA. Therefore, the flux is maximum when the area under consideration is perpendicular to the magnetic field. Suppose the magnetic field and the area vector are in opposite directions, then the angle between the two is 180o and the flux will be negative. Problem 1: A rectangular loop is 0.50 m long and 0.40 m wide. It is placed in a constant magnetic field of 0.3 T such that its area vector A makes an angle of 30° with B. Determine the magnetic flux through the surface. Solution: Given, B = 0.3 T θ = 30 ͦ l = 0.5 m w = 0.4 m A = l x w = 0.5 x 0.4 = 0.2 m2 Therefore, φ = BA cos θ or, φ = 0.3 T x 0.2 m2 x cos 30 ͦ or, φ = 0.052 Wb Problem 2: A magnetic field of 1.5 T passes perpendicular to a disc of diameter 6 cm. Find the magnetic flux passing through the disc. Solution: Given, B = 1.5 T d = 6 cm r = d/2 = 6/2 cm = 3 cm = 0.03 m A = πr2 = π x (0.03 m)2 = 0.0028 m2 We have, φ = BA or, φ = 1.5 T x 0.0028 m2 or, φ = 0.0042 Wb Magnetic Flux Density In the above equation, when A = 1, φ = B. Therefore, the magnetic flux density is defined as the flux passing through a unit cross-sectional area. Magnetic Field from Magnetic Flux By rearranging the above equation, we get Thus, the magnetic field is given by the flux per unit area perpendicular to the field. SI Unit: Wb/m2 where, ε: Induced emf N: Number of turns of the coil Δφ/Δt: Change in magnetic flux over time
Lenz’s Law
Suppose a loop of wire is placed in a changing magnetic field such that the magnetic flux passes through the wire. Then, Lenz’s law gives the direction of the induced current in the wire and the polarity of the induced emf. The induced current will generate an induced magnetic field, whose direction is given by the right-hand rule.
Gauss’s Law for Magnetism
Gauss’s law for magnetism states that the net magnetic flux coming out of a closed surface is zero. This statement gives an understanding of magnetic field sources. For example, all field lines in a bar magnet from the north pole must enter the south pole. A closed surface enclosing a bar magnet will have no flux coming out. Therefore, Gauss’s law for magnetism proves that a magnetic monopole does not exist.