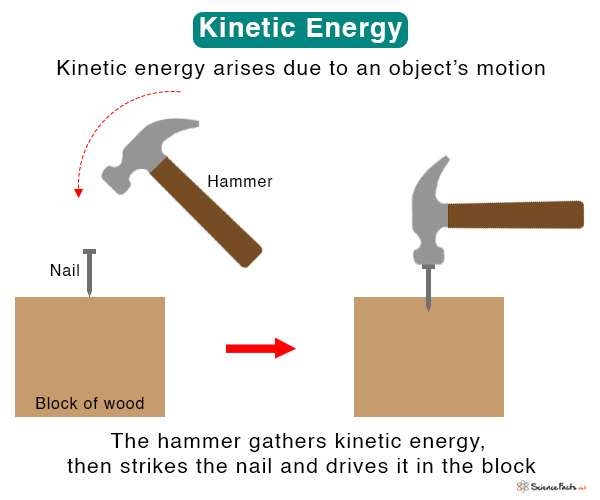
According to Newton’s First Law, an object at rest will stay at rest unless acted by force. When force is applied, it does work on the object. Work means the transfer of energy from one form to another. In this case, the form into which energy transforms is kinetic energy. The object attains kinetic energy and moves with a specific velocity.
Kinetic Energy Equation
Kinetic Energy Examples
Types of Kinetic Energy
Summary
Solved Problems
K.E. = ½ mv2 Where, K.E.: kinetic energy m: mass v: velocity SI Unit: Joule or J (1 J = 1 kg m2/s2) Cgs Unit: Erg (107 erg = 1 J) Dimensions: [ML2T-2] For the above equation, it is clear that increasing velocity increases kinetic energy. Similarly, an object with a higher mass will have higher kinetic energy.
Change in Kinetic Energy
An object can start from rest and acquire velocity. An object can also change its velocity during its motion. Suppose the object moves with a velocity vi, the initial velocity. A force alters its motion such that its velocity changes to vf, which is the final velocity. Then, the change in kinetic energy is, ΔK.E. = ½ mvf2 – ½ mvi2 Now, work is being done on the object to change its motion. The change of kinetic energy is equal to the work done W. Therefore, W = ΔK.E. This equation is known as the work-energy theorem.
Rotational Kinetic Energy
An object rotating about its axis also has kinetic energy. Its kinetic energy depends on angular velocity and moment of inertia. For rotational motion, the expression for kinetic energy is different from linear motion. The formula is, K.E. = ½ Iω2 Where, I: moment of inertia ω: angular velocity An example of rotational kinetic energy is a merry-go-round. Suppose an object executes both translational and rotational motion. In that case, the total kinetic energy is the sum of kinetic energy due to each motion. K.E.Total = ½ mv2 + ½ Iω2
Vibrational Kinetic Energy
A vibrating object has kinetic energy. For example, a spring oscillates with kinetic energy given by, K.E. = ½ kx2 Where, k: spring constant x: displacement
A bird flying in the airA ship sailing in the seaA car driving on the roadA rocket launching into spaceWater flowing down a streamPlanets orbiting around the sun with a gravitational forceA windmill with its blades rotatingA bullet fired from a gunAn oscillating pendulumAn archer releasing an arrow from a bowA roller coaster in descent
The following image shows a few examples of kinetic energy.
- Mechanical Energy: It is the energy associated with the mechanical movement of objects. Examples:
A bowling ball rolling down an alleyA soccer ball moving through the air
- Electrical Energy: Also known as electricity, it is caused by electron flow along a conductor. Examples:
A table lamp turned onElectrolysis
- Sound Energy: It is caused by the motion of vibrating air particles. When the vibrations reach the ears, the brain perceives them as sound. Examples:
Human voiceSound of drums
- Radiant Energy: It is caused by oscillating electric and magnetic fields, resulting in electromagnetic waves. Particles or waves carry the energy. Examples:
Light emitted by incandescent light bulbsRadiation emitted by X-rays
- Thermal Energy: Also known as heat energy, it is caused by atoms and molecules moving and colliding. The faster the atoms move, the hotter the object will be. Examples:
Boiling water in a panBaking food in an oven
Associated with a moving objectIncreases or decreases with the change in velocityGreater for heavier massCan transform into other types of energyMeasured in the unit of Joules
Soln.: Given, m = 2 kg v = 15 m/s Therefore, K.E. = ½ (2 kg) (15 m/s)2 Or, K.E. = 225 J P.2. Calculate the kinetic energy of a 78 kg person walking with a speed of 1.2 m/s? Soln.: Given, m = 78 kg v = 1.2 m/s K.E. = ½ mv2 Or, K.E. = ½ (78 kg) (1.2 m/s)2 Or, K.E. = 56.2 J P.3. Calculate the mass of an object moving at 25 m/s with a kinetic energy of 1500 J. Soln.: Given, K.E. = 1500 J v = 25 m/s The kinetic energy is, K.E. = ½ mv2 Or, m = 2 K.E./v2 Or, m = 2 x 1500 kg m2s-2 /(25 ms–)2 Or, m = 4.8 kg P.4. Work done by a force on a moving object is 150 J. The object was traveling at a speed of 2.5 m/s. Find the new speed of the object if the mass of the object is 1.5 kg. Soln.: Given, W = 150 J vi = 2.5 m/s m = 1.5 kg Therefore, W = ΔK.E. Or, W = ½ m (vf2 – vi2) Or, vf2 = 2W/m + vi2 Or, vf2 = 2 x 150 kg ms-1 /1.5 kg + (2.5 ms-1)2 = 206 m2/ss Or, vf = √206 m2/ss = 14.3 m/s