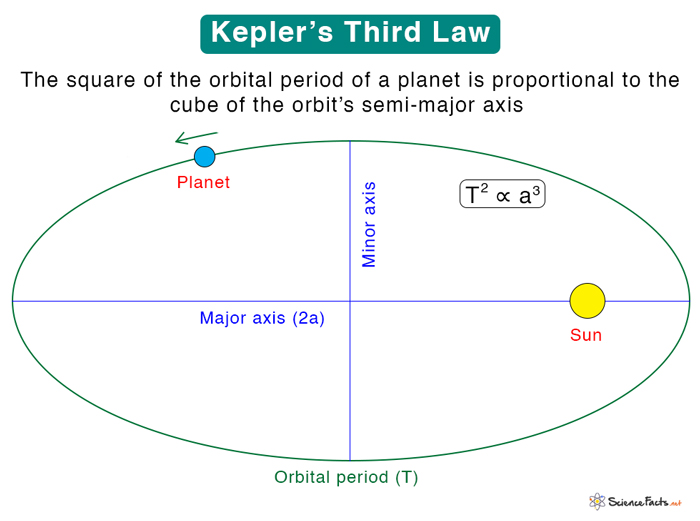
Kepler’s third law establishes a relationship between the time taken by a planet to complete one revolution and its distance from the Sun. According to this law, the orbital period increases rapidly with the orbit’s radius. The importance of the third law is that it has been successful in measuring the masses of the planets in the solar system. This law can also be applied to planets beyond the solar system, asteroids, comets, and artificial satellites. Another name for Kepler’s third law is the law of harmony. German astronomer and mathematician Johannes Kepler published this law in 1619.
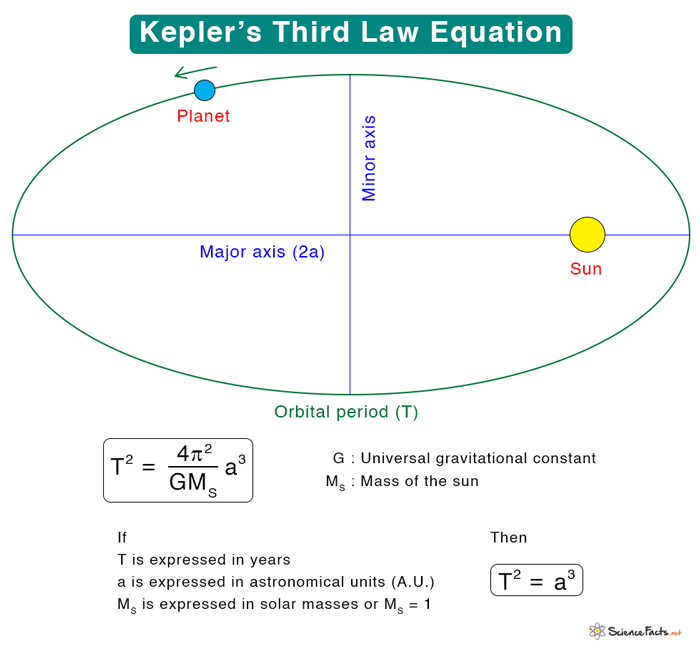
Equation
Kepler’s third law establishes the relationship between the orbital period and the distance of a planet’s orbit from the Sun. Kepler stated in his first law that the planets move around the Sun in elliptical orbits. The orbit’s size is represented by the semi-major axis a. Suppose T is the orbital period. Then, according to this law, Where k is the constant of proportionality.
Derivation
Newton showed in 1687 that Kepler’s third law was a direct consequence of his laws of motion and his law of gravity. To prove this and make the derivation easier, we make a few assumptions:
The planets’ orbits are circular rather than elliptical.The Sun is at the center of the orbits rather than the focus.
Newton’s law of gravity states that the force of attraction between the Sun and a planet is given by Where Ms : Sun’s mass Mp : Planet’s mass R : Distance between the planet and Sun G : Universal gravitational constant. In this case, R is assumed to be the radius of the orbit. When an object moves in a circle, there will be a centripetal force. When a planet moves with a velocity V, the centripetal force FC is given by The gravitational force provides the centripetal force. Therefore, However, the speed V is given by the distance the planet moves divided by the time it takes. For one complete revolution, this is given by Where 2πR is the circumference and T is the time taken to complete one revolution, known as the orbital period. Substituting for V, we get Replacing R with the semi-major axis a, This equation is the Kepler’s third law, where the constant of proportionality k is given by Thus, we have derived Kepler’s third law from Newton’s laws of motion and Newton’s law of gravity. Suppose T is expressed in Earth years a is expressed in astronomical units (AU) Ms is expressed in solar mass or Ms = 1 Then And The following table shows the orbital period in years and the semi-major axes in astronomical units (A.U.) of the solar system planets. It is observed that the ratio T2/a3 comes out to be close to 1.
Example Problems
Problem 1: Kepler’s third law says that T2/a3 is the same for all objects orbiting the Sun. Consider the dwarf planet Ceres in the asteroid belt that takes 4.6 years to orbit the Sun. Calculate the average Sun-Ceres distance. Solution: Given T = 4.6 y From Kepler’s third law T2 = a3 Or, a = (T)2/3 Or, a = (4.6)2/3 Or, a = 2.77 A.U. Problem 2: Jupiter takes 11.86 years to complete one revolution. What is its distance from the Sun in km? (1 A.U. = 1.5 x 108 km) Given T = 11.86 y From Kepler’s Law T2 = a3 Or, a = (T)2/3 Or, a = (11.86)2/3 Or, a = 5.2 A.U. = 5.2 A.U. x 1.5 x 108 km/A.U. = 7.6 x 108 km