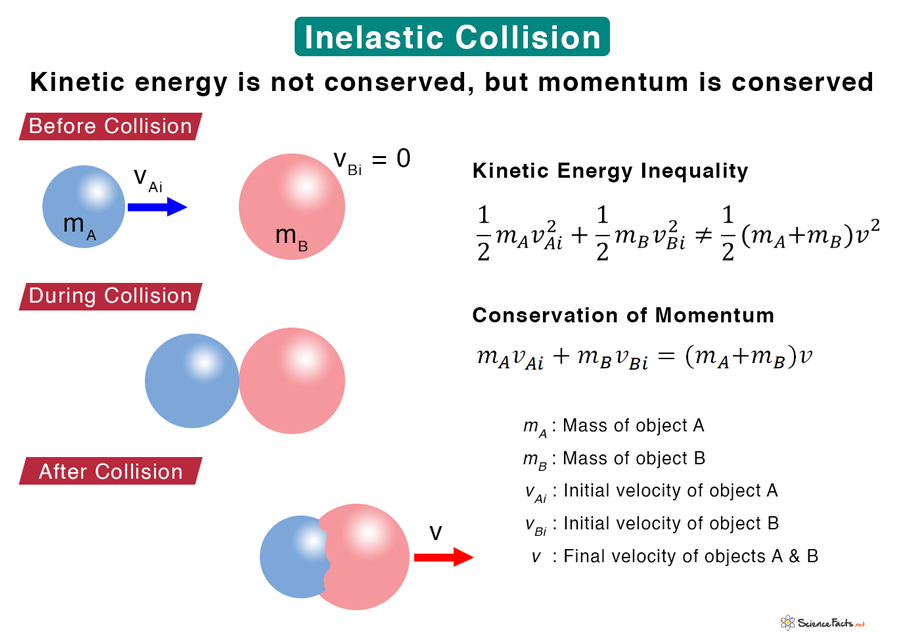
A perfectly inelastic collision, also known as a completely inelastic collision, loses the maximum amount of kinetic energy. In such a situation, objects stick together after the collision. For example, when a ball made out of mud is thrown at a wall, it sticks to it. In an inelastic collision, momentum is conserved. It means that the total momentum before the collision is the same as after.
Characteristics and Properties
Examples
Equations
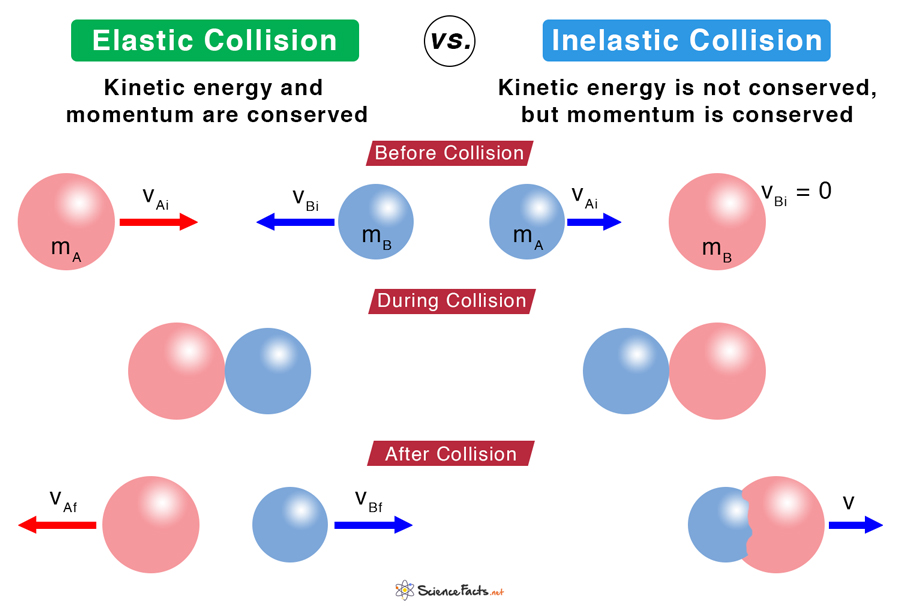
Elastic and Inelastic Collisions
Problems and Solutions
Total momentum remains the same before and after the collisionTotal kinetic energy does not remain the same before and after collisionKinetic energy is lost due to dissipative factors like sound, friction, and heatObjects may deform or dent or even stick together
The above equation gives the common velocity of the objects after the inelastic collision. Coefficient of Restitution The coefficient of restitution (CR) is the ratio between the final and the initial velocities of an object undergoing collision. It takes a value between 0 and 1, with 0 meaning a perfectly inelastic collision and 1 being perfectly elastic. The following equation gives the value. The coefficient of restitution of a golf ball on a steel surface is 0.9, and a billiard ball can be up to 0.98. a) What is the final velocity of the two vehicles in m/s? b) How much of the initial kinetic energy is lost to the collision? Solution: Given, mA = 2500 kg mB = 1500 kg vA = 60 km/hr = 60 km x 1000 m/km/(1 hr x 3600 s/hr) = 16.67 m/s vB = 0 a) The combined velocity is given by, v = (mAvA + mBvB)/(mA + mB) Or, v = (2500 kg x 16.67 m/s + 1500 kg x 0)/(2500 kg + 1500 kg) Or, v = 10.42 m/s b) Kinetic energy before collision (K.E.)i = ½ mAvA2 + ½ mBvB2 = ½ x 2500 kg x (16.67 m/s)2 + 0 = 347361 J Kinetic energy after collision (K.E.)f = ½ (mA + mB)v2 = ½ x (2500 kg + 1500 kg) x (16.67 m/s)2 = 217152 J Therefore, fraction of energy lost is 1 – (K.E.)f/(K.E.)I = 217152 J/347361 J = 0.38