Inductance Formula
Inductance and Shape of Inductors
Types of Inductance
Factors Affecting Inductance
Uses and Applications
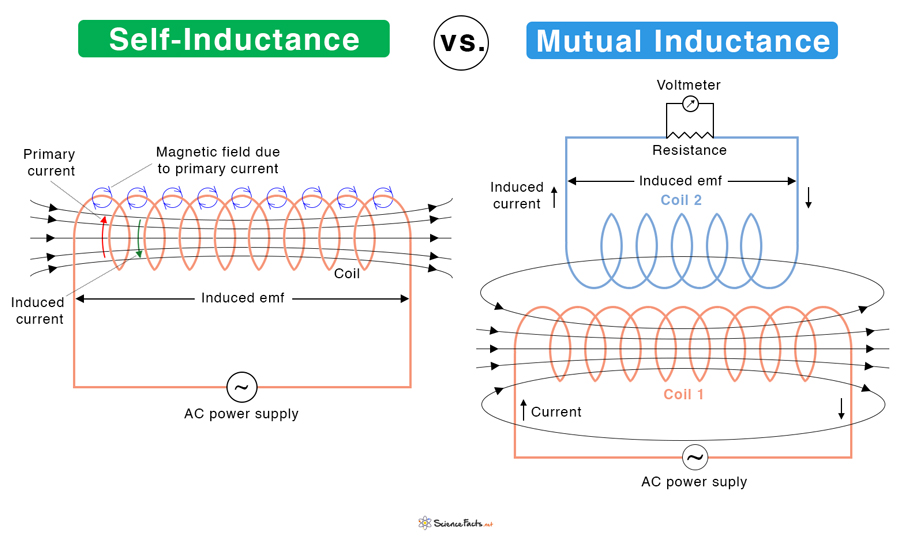
What is the Difference Between Self-inductance and Mutual Inductance
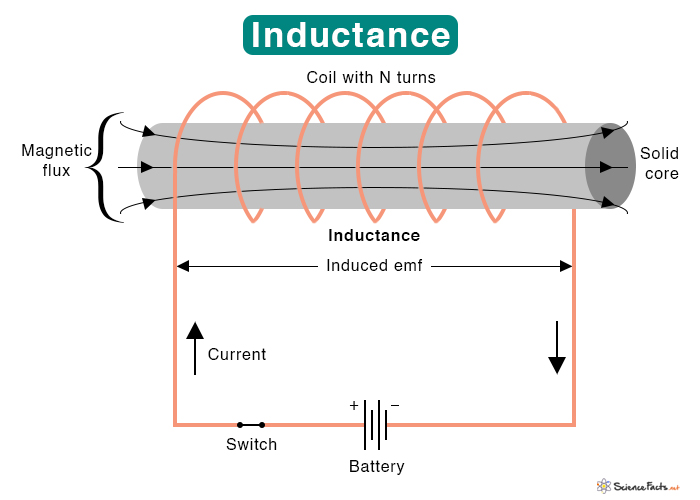
To measure the inductance, we use a device called an inductor in the electrical circuit. The SI unit of inductance is Henry or H, named after American scientist Joseph Henry. He discovered electromagnetic induction around 1831. Some inductors are made up of a single wire and are wound into a self-supporting coil. Other inductors consist of a wire wound into a coil around a long solid core, circular core, or rectangular core made of soft iron. A soft iron core chokes the current rise more effectively than air, increasing the inductance.
1. Self-Inductance
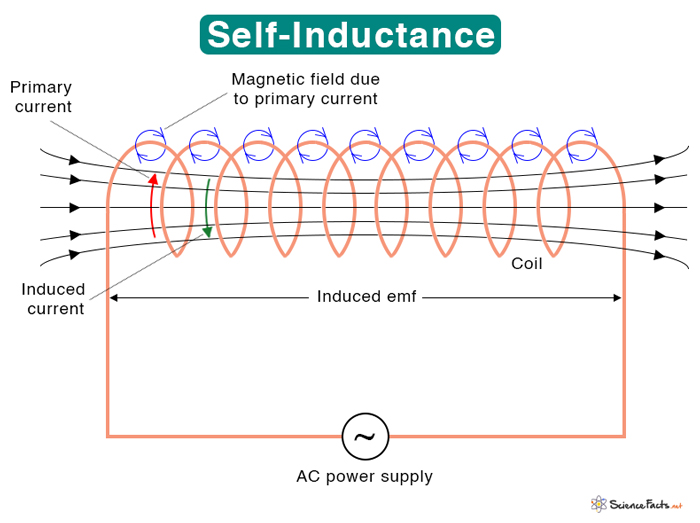
If the emf is induced in the same coil as the flowing current, it is known as self-inductance. An example of a device where self-inductance occurs is a choke. The symbol L denotes it.
Equation
The self-inductance L can be found in terms of the flux φ, number of turns of the coil N, and current I. Using the above equation, the self-inductance can be calculated for the solenoid and toroid.
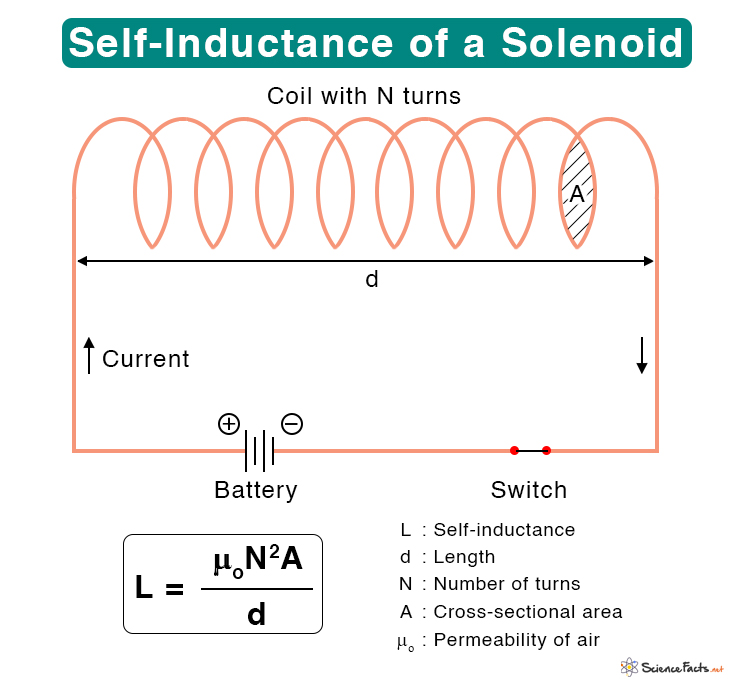
- Solenoid The following equation gives the self-inductance of a solenoid. Where N : Number of turns A : Cross-sectional area d : Length μo: Permeability of air
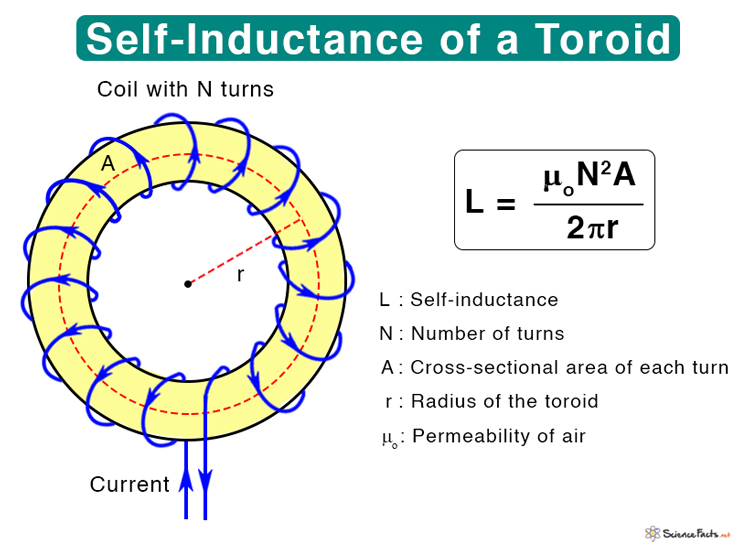
- Toroid The following equation gives the self-inductance of a toroid. Where N : Number of turns A : Cross-sectional area r : Radius of the toroid μo: Permeability of air Suppose the coil is wrapped around a solid core instead of a hollow one. In that case, air permeability is replaced by the permeability of the core material and denoted by μ.
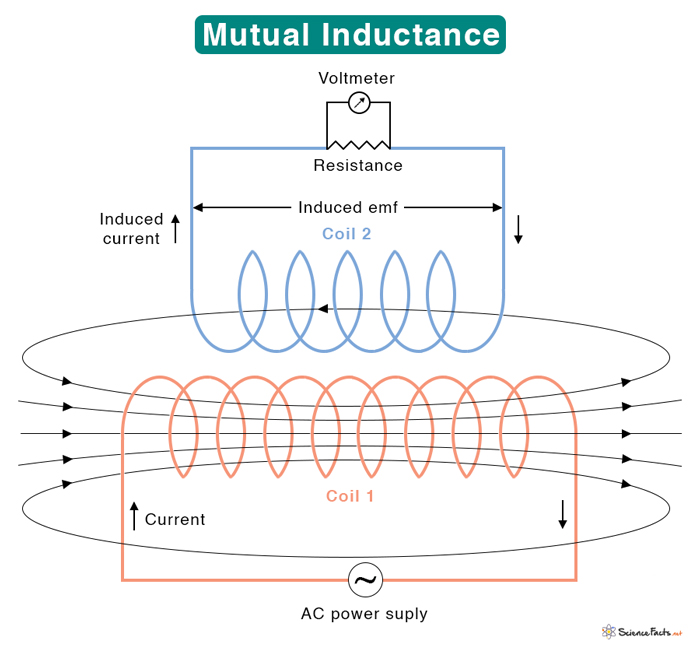
2. Mutual Inductance
If the emf is produced in another coil placed next to the first, it is known as mutual inductance. Mutual inductance occurs in a transformer, generator, and motor. The symbol M denotes it.
Equation
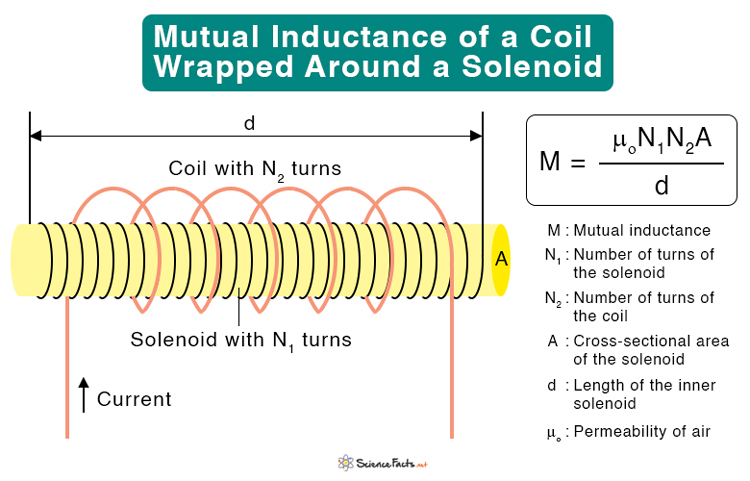
Suppose the second coil has N2 turns and the flux passing through it due to current I1 in the first coil is φ21. The following equation gives the mutual inductance. Based on the above equation, the mutual inductance can be calculated for different arrangements of coils. Mutual-inductance Between a Coil and a Solenoid The following equation gives the mutual inductance of a coil wrapped around a solenoid. Where N1 : Number of turns of the solenoid N2 : Number of turns of the coil A : Cross-sectional area of the solenoid d : Length of the solenoid 2. Cross-sectional area of the coil: It is directly proportional to the cross-sectional area of the coil. The higher the area of the coil, the higher the inductance. 3. Number of turns: It is directly proportional to the number of turns square. Hence, the higher the number of turns, the higher the inductance. 4. Permeability of the core: The permeability of the core material allows the magnetic field to form inside the core. The inductance is directly proportional to the permeability. The higher the permeability, the higher will be the inductance.