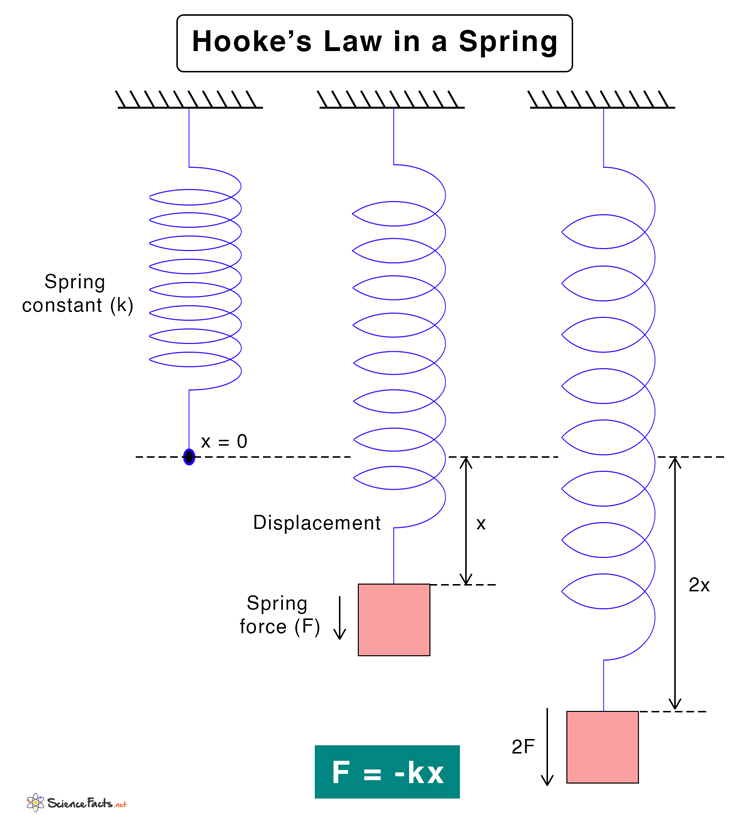
Historically, the law has been named after British physicist Robert Hooke. He established a relationship between force and displacement in 1660 and published it in 1678.
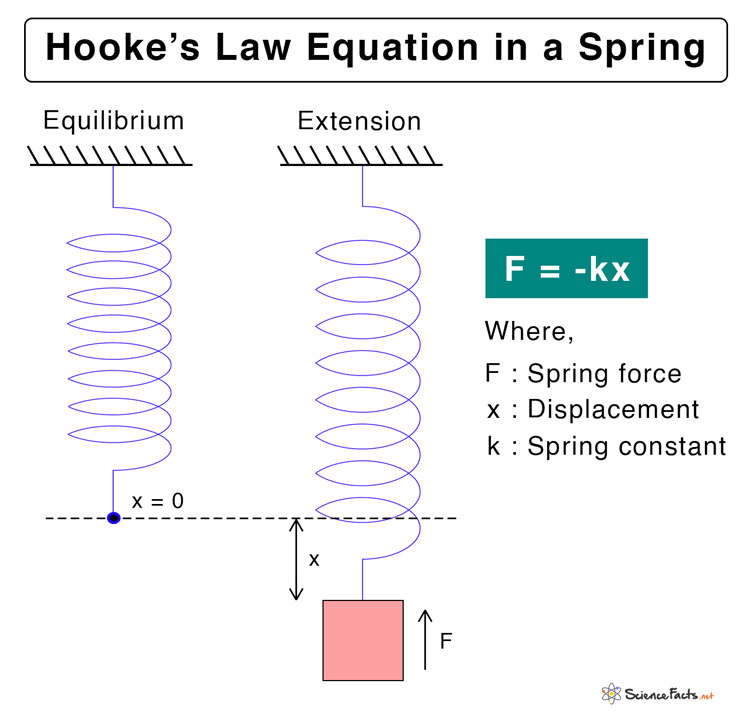
Hooke’s Law Equation
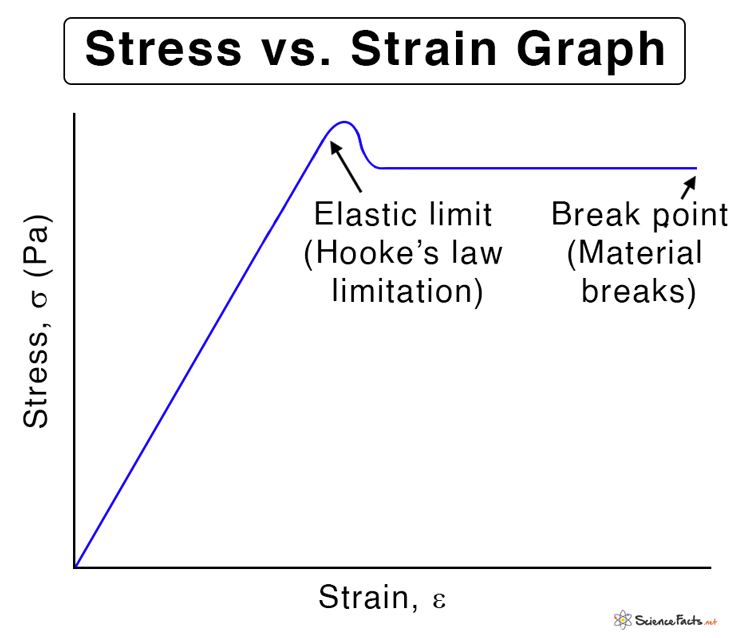
Limitations of Hooke’s Law
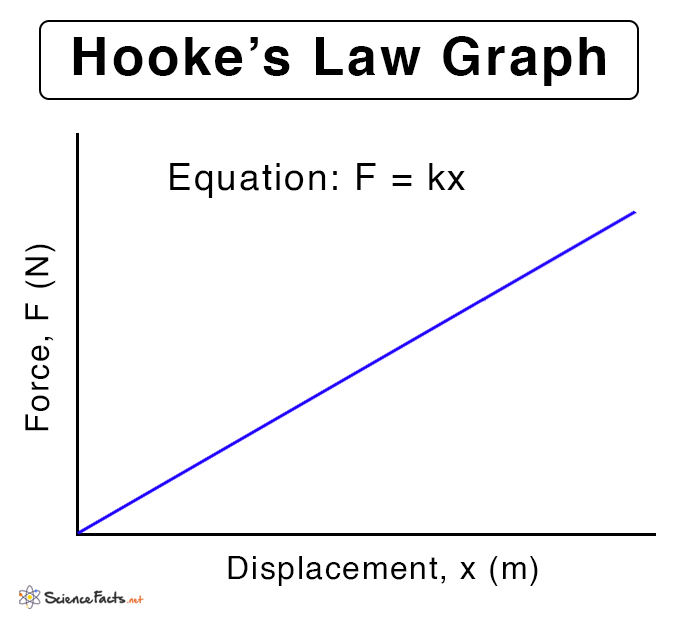
Hooke’s Law Graph
Stress and Strain in Hooke’s Law
Applications of Hooke’s Law
Solved Examples and Problems
F ∝ x Or, F = -kx SI unit of Hooke’s law: Newton or N (kg.m.s-2) Here, k is known as the force constant or spring constant. The negative sign is because the restoring force is in the opposite direction to the displacement. It is responsible for bringing back the spring to its equilibrium position. This equation applies to both compression and extension of spring. The spring force can be measured using a spring tester or a weighing scale. The magnitude of the force is given by, F = kx Spring Constant The magnitude of the spring constant is given by, k = F/x Suppose F = 1 N and x = 1 m, then k = 1 N/ 1 m = 1 N/m Therefore, the spring constant is defined as the force required to displace the spring by one meter. It has a unit of Newton per meter (N/m) and a dimension given by MT-2. Elastic Energy When spring is deformed, work is being done on it. This work is manifested in the form of elastic potential energy stored by the spring. By definition, work done is the change in potential energy. As the deformation is removed, energy is released as the potential energy is converted into kinetic energy. The work done W in compressing or extending the spring by a distance x is given by, W = ΔPE = ½kx2 Stress = Modulus of Elasticity x Strain
Stress-Strain Equation
An object can be deformed in different ways. The stress and strain can be of two types – 1. longitudinal or normal and 2. shear or torsion. Based on the types, Hooke’s law can be written as follows.
- Normal or Longitudinal σ = E x ε Where, σ is the normal or longitudinal stress ε is the normal or longitudinal strain E is Young’s modulus or modulus of elasticity
- Shear or Torsion τ = G x γ Where, σ is the shear or torsional stress ε is the shear or torsional strain G is the shear modulus Soln. Given, k = 15 N/m x = 15 cm = 0.15 m Formula: F = kx Therefore, F = 15 N/m x 0.15 m = 2.25 N P.2. A spring is pulled to 12 cm and held in place with a force of 550 N. What is the spring constant of the spring? Soln. Given, F = 550 N x = 12 cm = 0.12 m Formula: F = kx Therefore, k = F/x or, k = 550 N/0.12 m = 4583 N/m P.3. What is the force required to stretch a 15 cm-long spring, with a spring constant of 80 N/m, to a length of 17 cm? Soln.: Given, l1 = 15 cm l2 = 17 cm k = 80 N/m Therefore, x = l2 – l1 = 17 cm – 15 cm = 2 cm = 0.02 m From Hooke’s law equation, F = kx F = 80 N/m x 0.02 m = 1.6 N P.4. What is the spring constant of a spring that needs a force of 4 N to compress from 50 cm to 45 cm? Soln.: Given, F = 4 N l2 = 50 cm l1 = 45 cm Therefore, x = l2 – l1 = 45 cm – 50 cm = – 5 cm = – 0.05 m or, |x| = 0.05 m From Hooke’s law equation, F = kx or, k = F/x = 4N / 0.05 m = 80 N/m