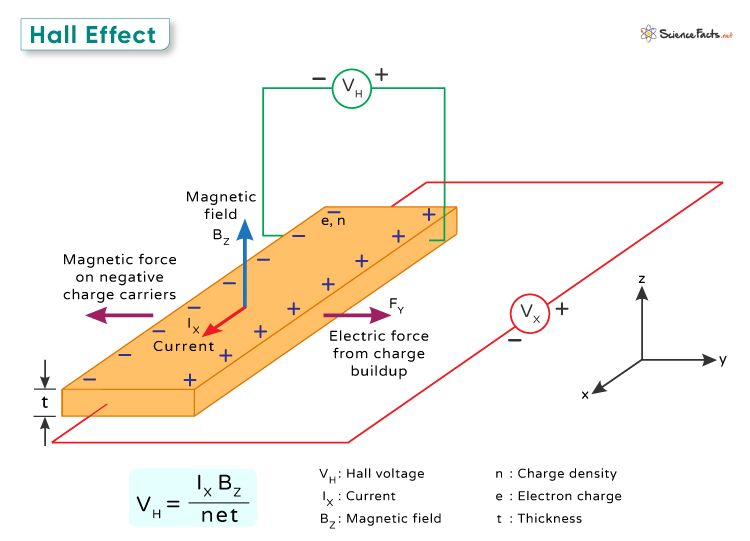
This phenomenon demonstrates how electric and magnetic fields can influence the movement of charged particles in a material. By studying the Hall effect, scientists can learn important information about the charge carriers, such as electrons, within the material. This effect was discovered by American Physicist Edwin Hall in 1879.
Principle
Equation
Hall Coefficient
Applications
Example Problems
This sideways push is key to understanding the Hall Effect. Imagine electrons moving through a conductor because of an electric field that drives them forward. When a magnetic field is added, it exerts a sideways force on the electrons, making them move to one side of the conductor. As electrons gather on one side, they create a negative charge buildup, leaving a positive charge on the other side. This separation of charges creates an electric field inside the conductor that opposes further electron movement. This process continues until the electric force from the charge buildup balances the magnetic force from the Lorentz force. The result is a stable situation where the forces are balanced, and a voltage, called the Hall voltage, is generated across the conductor. Where
VH is the Hall voltageIx is the current flowing through the conductorBz is the applied magnetic fieldn is the number of charge carriers per unit volumee is the value of the electric charget is the thickness of the conductor
Where
RH is the Hall coefficientEy is the electric field due to the Hall effectjx is the current density
The Hall coefficient provides crucial insights into the material’s electronic properties. Its interpretation extends beyond a mere numerical value. It reflects the density and mobility of charge carriers within the material. Solution The Hall voltage can be calculated using the formula: Rearranging the formula for n, we get: Given data:
Ix = 2 ABz = 0.5 TVH = 0.1 Vt = 1 cm = 0.01 m (converted to meters)
Substituting the values, we get: The charge carrier density of the metal is 6.25 x 1021 m–3.