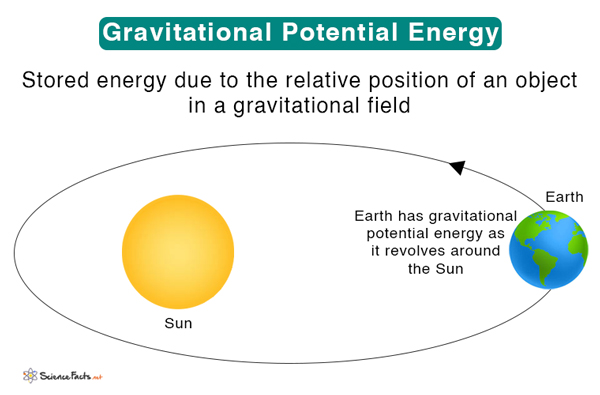
Gravitational potential energy is also associated with the Earth, which we know as gravity. An object at a specific height above the Earth’s surface possesses gravitational potential energy. When the object is released, its potential energy is converted into kinetic energy. The sum of the two always remains constant because of the conservation of energy law. Gravitational potential energy helps us to understand the motion of planets. When scientists send spacecraft to other planets, they can precisely calculate how much energy is needed to fuel them. English mathematician and physicist Isaac Newton published his comprehensive theory of gravitation in 1687.
Examples
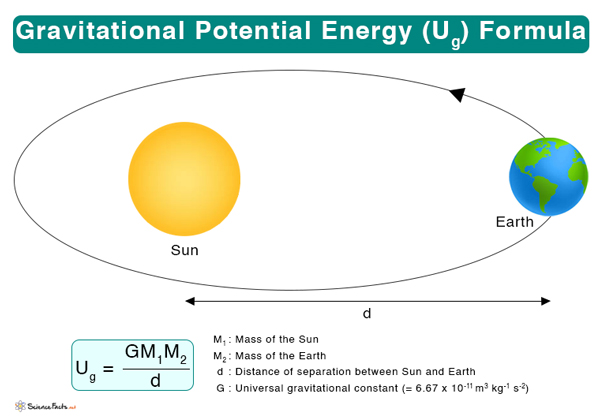
Formula
Why is Gravitational Potential Energy Negative
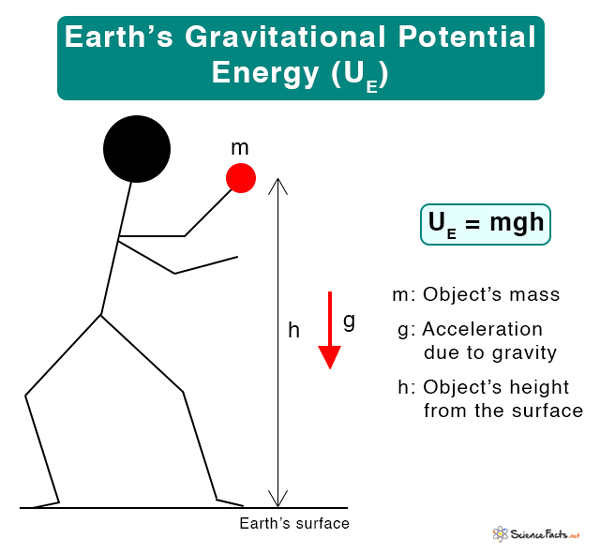
Earth’s Gravitational Potential Energy
Derivation
Gravitational Potential
Where Ug: Gravitational potential energy M1: Mass of the source object M2: Mass of the test object d: Distance of separation between the two objects G: Universal gravitational constant (= 6.67 x 10-11 m3 kg-1 s-2) Symbol: Ug SI Unit: Joules Dimension: [ML2T-2] Where UE: Gravitational potential energy due to Earth m: Mass of the object h: Height of the object above the Earth’s surface g: Acceleration due to gravity (=9.81 m/s2) From the above equation, it is clear that the gravitational potential energy due to Earth depends upon two factors – the object’s mass and height. The heavier the object, the greater the energy. Similarly, the higher the object, the higher its potential energy. When the object is raised from the ground to a height h, the change is gravitation potential energy is This change is equal to the work done in lifting the object. Where Fg is the gravitational force. At a distance x from the source object, it is given by Replacing Fg in the dW equation Integrating the above from infinity to d Since the work done is the change in gravitational potential energy, we have