Gravitational force is non-contact since there is no contact between the objects. It is centripetal since it is directed toward the center of the orbit around which the object moves. It is responsible for keeping the body in orbit. The revolving body feels a tug that is directed away from the center. This tug is called the centrifugal force. The gravitational force is the weakest of all fundamental forces. Many famous scientists have made significant contributions to the field of gravitation. In the early 17th century, Italian astronomer Galileo Galilei found that all objects accelerate equally toward the center of the Earth. English mathematician Isaac Newton was the first to discover the laws of gravitation in his 1687 seminal work.
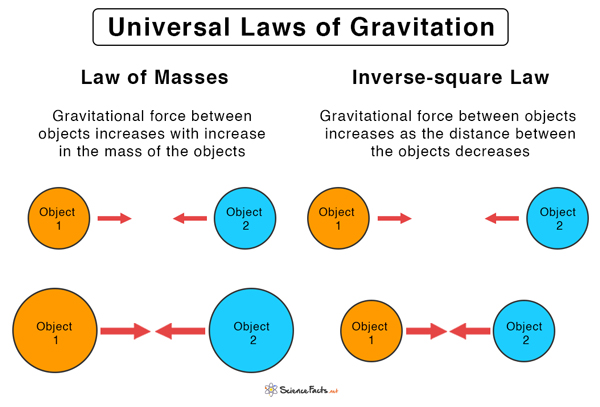
Universal Laws of Gravitation
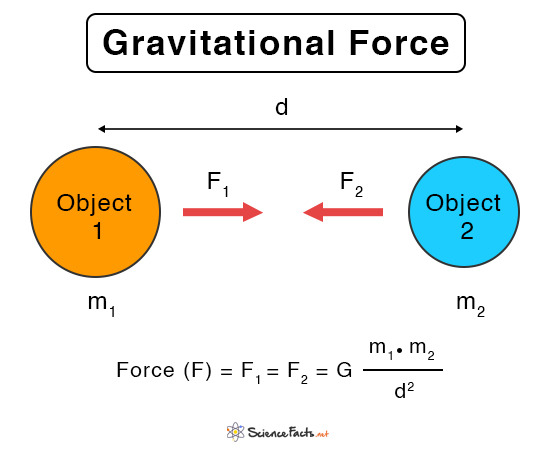
Properties of the Gravitational Force
Examples of Gravitational Force
Advantages and Disadvantages of the Gravitational Force
Gravitational Force Problems and Solutions
directly proportional to the product of the massesinversely proportional to the square of the distance between their centers
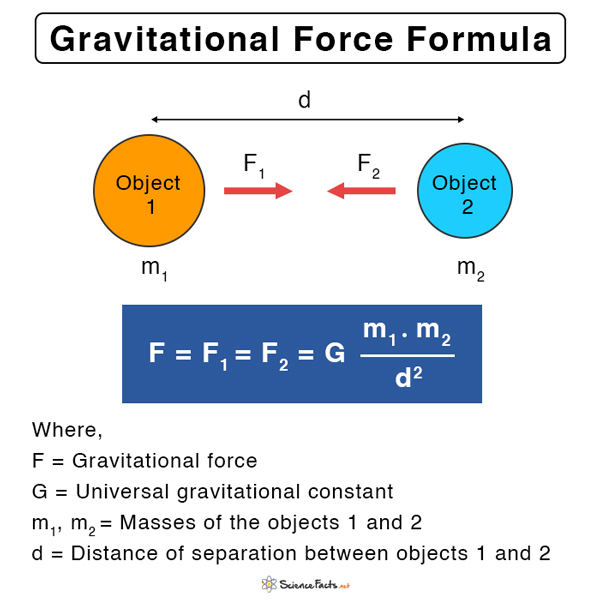
These are the two factors that affect the gravitational force. The value is high for massive objects and when the bodies are closer to one another. General Formula for Gravitational Force Suppose M1 and M2 be the masses of the two bodies, and R be the distance of separation between their centers. The following equation gives the gravitational force between the two objects. Unit of Gravitational Force: N or Newton Here, G is called the universal gravitational constant. It is an empirical physical constant with a value of 6.67 X 10-11N.m2/kg2. Its dimensional formula is M-1L-3T-2. By knowing the masses M1 and M2 and their distance of separation d, it is possible to calculate the magnitude of F.
AttractiveNon-contactLong-rangeIt does not require a mediumDirectly proportional to the product of the masses of the objectsInversely proportional to the square of the distance of separation between the objectsA constant value on the surface of the EarthWeakest of all fundamental forcesActs along the line joining any two bodies
1. Gravitational Force of the Earth
Earth exerts a gravitational force on every object, a phenomenon known as gravity. Gravity holds us on the surface and does not let us float freely in the air. We exert the same force on Earth that the Earth exerts on us. However, the Earth is so massive that it is unperturbed. An object suspended in air will fall freely towards the center of the Earth when released. The difference between gravitational force and gravity is that the former is applied to any two objects in the universe. Gravity is the force between Earth and any other object close to Earth, including on its surface. The force of gravity is given by, Where ME is the mass of the Earth, m is the mass of an object, and RE is the Earth’s radius. If the object is at an altitude h above the surface of the Earth, then the equation modifies to From the above equation, it is quite clear that the Earth’s gravitational force vanishes when h →∞, or at large distances from the surface. According to Newton’s second law of motion, force is given by mass m multiplied by acceleration a. Therefore, Comparing equations (2) and (4), The above term is called acceleration due to gravity. It has a value of 9.81 m/s2 on the surface of the Earth. Multiplying g by the mass of a person gives the weight W of the person. The acceleration due to gravity in space is zero, which is why astronauts feel weightless and float freely. The following expression gives the work done by Earth’s gravitational force when an object of mass m falls from a height h above the Earth’s surface. This work is the change in the object’s potential energy as the object falls through the air. Satellites orbit around the Earth in fixed orbits due to the gravitational pull. Without gravity, the satellites would have been flung away into space. The gravity in the polar region is higher than that at the equator. The reason is that the poles are closer to the center of the Earth than the equator.
Gravitational Force Between Earth and Moon
The Moon revolves around the Earth because gravitational forces hold them together. To calculate this force, we put their masses and the distance between their two centers in equation (1). Mass of the Earth: ME = 6.0 x 1024 kg Mass of the Moon: MM = 7.35 x 1022 kg The average distance between the Earth and Moon, REM = 3.844 x 108 m Universal gravitational constant, G = 6.67 x 10-11 Nm2/kg2 From equation (1), Thus, the gravitational force between the Earth and Moon is 2 x 1020 N.
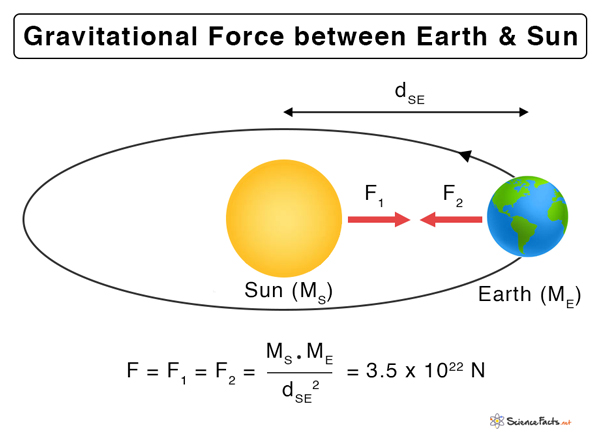
2. Gravitational Force of the Sun
The Sun has a gravitational force due to its mass, which is so large that its influence extends vastly. All planets revolve around the Sun in elliptical orbits due to this attractive force. The gravitational force between the Sun and Earth can be calculated using equation (1). Mass of the Sun: Ms = 2.0 x 1030 kg Mass of the Earth: ME = 6.0 x 1024 kg The average distance between the Sun and Earth, RSE = 1.5 x 1011 m Universal gravitational constant, G = 6.67 x 10-11 Nm2/kg2 From equation (1), Thus, the gravitational force between the Sun and Earth is 3.5 x 1022 N. Likewise, the gravitational force between the Sun and other planets will depend upon their masses and distances.
3. Gravitational Force of the Planets
All planets of the solar system have their gravitational force. The values of the acceleration due to gravity are given below.
Mercury: 3.7 m/s2Venus and Uranus: 8.87 m/s2Mars: 3.71 m/s2Jupiter: 24.79 m/s2Saturn: 10.44 m/s2Neptune: 11.15 m/s2
Besides, the gravity of the Moon is 1.62 m/s2. When compared to Earth, it is about 1/6th.
Constant on the surface of the EarthIt keeps the muscles and bones workingAllows Earth to retain its atmosphereAllows water dams to store energy
Here are some of its disadvantages.
It makes it difficult to travel to outer space as rockets have to overcome the force of gravityIt makes us fall and get hurtLimits the height of tall buildings during constructionHard on the bones and joints as a person ages
Solution: Given M1 = 110 kg M2 = 130 kg d = 80 cm or 0.8 m F = G M1 M2 / d2 = 6.67 x 10-11 N.m2/kg2 x 110 kg x 130 kg / (0.8)2 = 1.5 X 10-6 N