In other words, the Fermi level is like a dividing line that helps us understand how electrons are distributed in a material. Below the Fermi level, energy levels are mostly filled with electrons, and above it, energy levels are mostly empty. The following representative image shows the position of the Fermi level in an intrinsic semiconductor. Fermi level is named after Italian-American physicist Enrico Fermi, who was the first one to propose the concept.
Introducing Fermi Energy
Fermi Level Equation
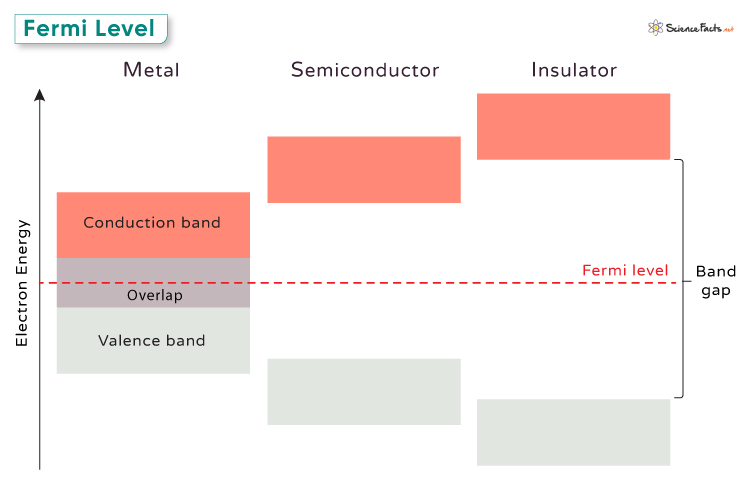
Fermi Level in Metals, Semiconductors, and Insulators
Also, the Fermi level can change with temperature and the presence of impurities (during semiconductor doping). However, the Fermi energy does not change because it is defined by the coldest state of the solid. Where: – f(E) is the Fermi-Dirac distribution function, representing the probability of finding an electron with energy E. – E is the energy of the electron. – EF is the Fermi level. – kB is Boltzmann’s constant. – T is the temperature in Kelvin. At thermal equilibrium, the Fermi level represents the energy level at which f(E) = 0.5. This means that the energy level in question is exactly at the Fermi level, indicating a 50% probability of being occupied by an electron at an absolute zero temperature.
Semiconductors
In semiconductors, the position of the Fermi level depends on whether the substrate is doped or undoped. In an intrinsic semiconductor (undoped), the Fermi level lies close to the middle of the band gap. The band gap is the energy range between the valence band (where electrons are bound to atoms) and the conduction band. When an extrinsic semiconductor is doped with impurities, the position of the Fermi level changes within the electron structure. It shifts either towards the conduction band (for n-type doping) or towards the valence band (for p-type doping). This movement of the Fermi level affects the semiconductor’s conductivity, allowing it to be used in electronic devices such as transistors and diodes.
Insulator
In insulators, the Fermi level lies within the band gap, far from the valance and the conduction bands. As a result, insulators have very low electrical conductivity since there are no available states for electrons to conduct through at the Fermi level. Instead, electrons are tightly bound to their respective atoms, requiring a significant amount of energy to transition into the conduction band.