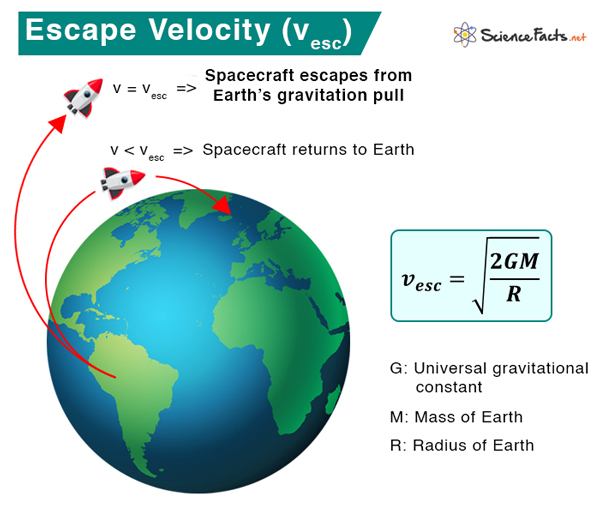
Escape velocity is the speed required for an object to be projected to overcome the Earth’s gravitational force. The object escapes from Earth’s surface into space without ever falling back.
Formula
Escape Velocity of Earth
Derivation
Where vesc is the escape velocity G is the universal gravitational constant (= 6.67 x 10-11 m3 ˑ kg-1 ˑ s-1) M is the mass of the earth (= 5.972 x 1024 kg) R is the radius of the earth (= 6.371 x 106 m) Therefore, the minimum velocity required to project an object from Earth’s surface to escape the gravitational pull is 11.182 km/s or 25,000 mph. Scientists use this value to send rockets into space.
Example Problem
If the mass of Mars is 6.41 x 1023 kg and its radius is 3.39 x 106 m, what is the escape velocity of an object launched from Mars? Solution Given MMars = 6.41 x 1023 kg RMars = 3.39 x 106 m G = 6.67 x 10-11 m3 ˑ kg-1 ˑ s-1 The escape velocity from Mars is The following table lists the escape velocities of several planets, the sun, and the moon. Where m is the object’s mass and v is its velocity. The gravitational potential energy on the surface of the earth is From the law of conservation of energy, the kinetic energy comes from the gravitational potential energy. In the escape velocity calculation, we assume no friction with the Earth’s atmosphere. After achieving the escape velocity, the object does not require any impulse to escape from Earth’s gravitational field. The object achieves zero velocity asymptotically at an infinite distance from the Earth’s surface, never to return.