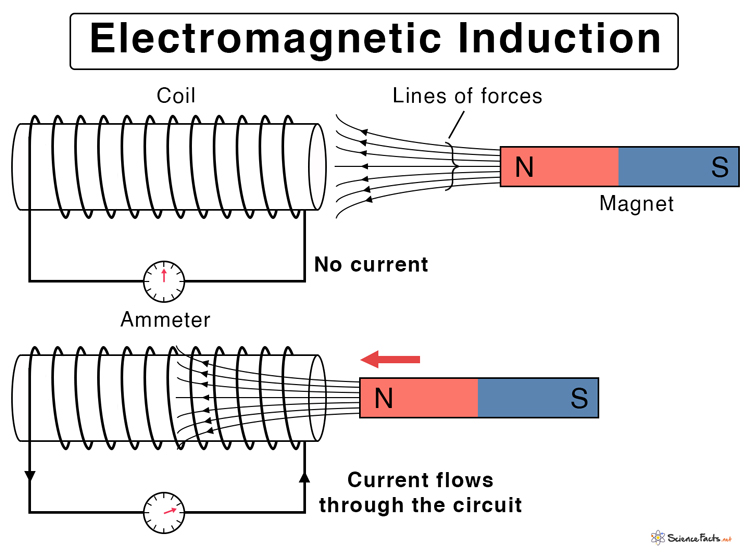
The magnetic field comes from a permanent magnet like a bar magnet. The phenomenon is called induction because there is no physical contact between the conductor and the magnet. The magnetic lines of force pass through air or medium if the coil is wrapped around a metallic core. A condition of electromagnetic induction is that there should be a relative motion between the conductor and the magnet.
Who Discovered Electromagnetic Induction
English physicist Michael Faraday discovered electromagnetic induction in 1831. Scottish physicist and mathematician James Clerk Maxwell developed the mathematical equations and published them in 1865. These equations are today known as Maxwell’s equations.
How does Electromagnetic Induction Work
Laws of Electromagnetic Induction
Examples and Applications of Electromagnetic Induction
Advantages of Electromagnetic Induction
Example Problems and Solutions
Magnetic Flux Equation Suppose the bar magnet a field of strength B. Consider a two-dimensional area A in space such that the lines of force pass through this area and make an angle θ with the area vector. Then, the area projected on a plane perpendicular to the field is A cos θ. The magnetic flux φ is defined as the product of the field and the projected area. φ = BA cos θ When the north pole is brought closer to the coil, the flux increases and will continue to increase as long as the magnet is in motion. The change in magnetic flux over time results in an induced current. If an ammeter is connected to the two ends of the coil, it will register a current. The current will continue to flow as long as the magnet is moving. If the magnet is retracted from the coil, the induced current will change direction. Faraday’s Law Equation Suppose the coil has N turns. It is placed in a magnetic field such that dφ/dt represents the flux rate. The formulas for induced emf ε are given by, ε = – N dφ/dt (continuous) ε = – N Δφ/Δt (discrete) SI Unit of EMF: Volts The negative sign is because the induced emf opposes the very reason causing it, which is dictated by Lenz’s law. Factors that Effect Electromagnetic Induction
- Number of Turns: The induced voltage is directly proportional to the number of turns of the wire. Therefore, the higher the number of turns, the higher is the voltage produced.
- Changing Magnetic Field: The induced voltage is directly proportional to the flux rate. Changing the magnetic flux affects the induced voltage. This change can be done by moving the magnet closer to or away from the coil and vice-versa.
2. Lenz’s Law
Faraday’s law does not state anything about the conservation of energy. Lenz’s law can explain the negative sign in Faraday’s law equation. Lenz’s law states that “The polarity of the induced emf is such that it opposes the change in magnetic flux that produced it.” In other words, an induced current will always oppose the motion that started it in the first place. Therefore, Lenz’s law can determine the direction of induced current. Lenz’s law is named after German physicist Heinrich Friedrich Lenz after he deduced it in 1834.
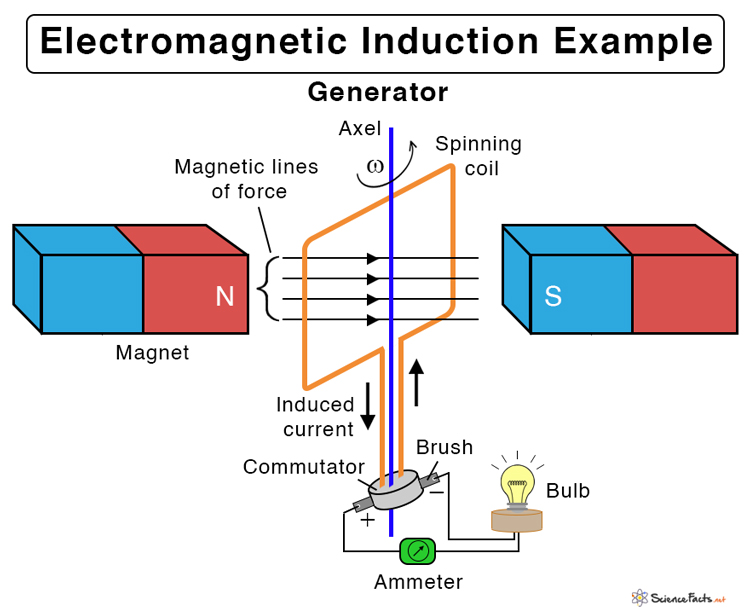
Electric generator: It converts kinetic energy into electrical energy and produces electricity in power plants. The electricity is then supplied to homes.
Electric transformer: It changes the voltage and comes in two types – step up and step down. A step-up transformer increases the voltage, while a step-down transformer decreases the voltage.Dynamo: It is a small generator consisting of a permanent magnet that is rotated inside a fixed coil by the movement of a bicycle wheel.Inductance: It is a simple coil with a ferromagnetic core and is usually a part of an electrical circuit. It stores energy in the magnetic field of the coil when current passes through it.
Cheap, simple, reliable, efficient, and controllableMechanical energy can be converted directly into electrical energyProduces electric current and powers homes
Soln. Given, N = 50 B = 2 Wb m-2 A = 150 cm2 = 150 x 10-4m2 = 0.015 m2 θ = 45˚ Δt = 0.3 s Initial flux: φi = BA cos θi = 2 Wb m-2 x 0.015 m2 x cos 45˚ = 0.021 Wb Final flux: φf = BA cos θf = = 2 Wb m-2 x 0.015 m2 x cos 0˚ = 0.03 Wb Therefore, Δφ = φf – φi = 0.03 – 0.021 = 0.009 Wb Therefore, the magnitude of induced emf is, |ε| = N Δφ/Δt = 50 x 0.009 Wb/0.3 s = 1.46 V P.2. A uniform magnetic field is normal to the plane of a circular loop 15 cm in diameter and made of copper wire of diameter 3 mm. (a) Calculate the resistance of the wire (R = ρl/A, the resistivity of copper: ρ = 1.68 x 10 -8 Ωm). (b) At what rate must the magnetic field change with time if an induced current of 15 A forms in the loop? Ans. (a) Given, d = 3 mm = 3 x 10-3 m ρ = 1.68 x 10 -8 Ωm D = 15 cm = 0.15 m Length of the wire = πD Cross-sectional area of the wire = πd2/4 Therefore, R = ρl/A = ρπD/(πd2/4) = 4ρD/d2 = 4 x 1.68 x 10 -8 Ωm x 0.15 m / (3 x 10-3 m)2 = 0.00112 Ω = 1.1 x 10-3 Ω (b) Given, I = 15 A R = 1.1 x 10-3 Ω N = 1 Therefore, V = IR = 15 A x 1.1 x 10-3 Ω = 0.0168 V From Faraday’s law, |ε| = Δφ/Δt Or, Δφ/Δt = 0.0168 V Or, Δ(BA)/Δt = 0.0168 V Or, ΔB/Δt = 0.0168 V/A =0.0168 V/(πD2/4) = 0.0168 V/(π(0.15m)2/4) = 0.95 V/m2 = 0.95 (V.s/m2).(1/s) = 0.95 T/s