Electrical Potential Energy Formula
Example Problems and Solutions
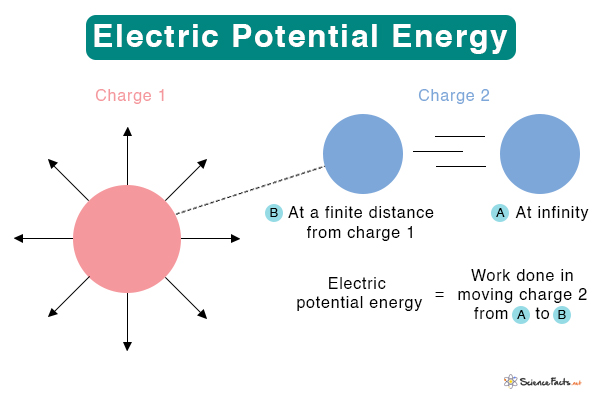
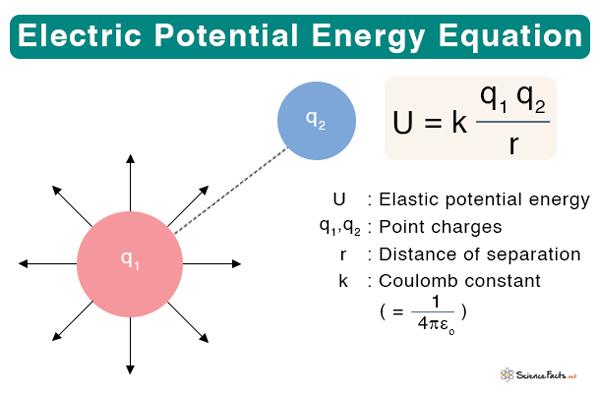
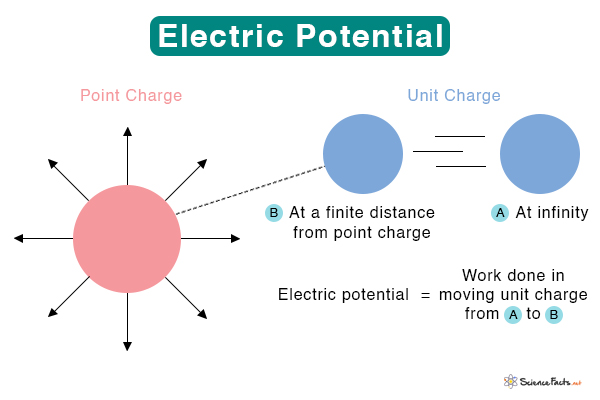
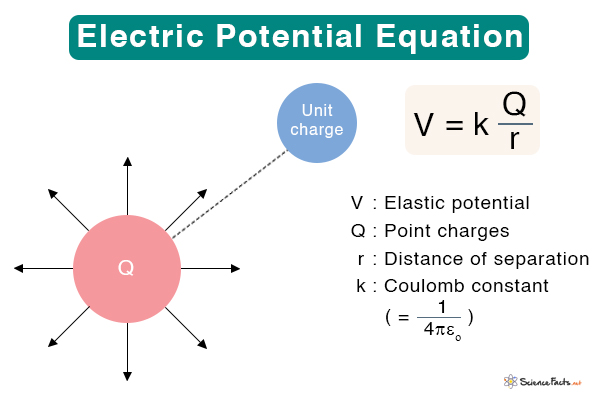
Suppose q1and q2are the magnitudes of the two charges and r is the separation distance between them. Then, the electric potential energy U is given by U ∝ q1q2/r Or, U = kq1q2/r Where k is a proportionality constant known as Coulomb constant, given by k = 1/(4πεo), whose value is 9 x 109 N m2/C2. SI Unit: Joule (J) Dimension: [ML2T-2] Symbol: U The electric potential energy per unit charge is known as electric potential. It can be obtained by dividing the electric potential energy by the magnitude of the test charge. V = U/q1 Or, V = kq1/r Replacing k by 1/(4πεo) and q1 by Q, we get the formal expression of the electric potential. V = Q/(4πεor) Unit: Volt (V) or Joule/Coulomb (J/C) Dimension: [ML2T-3A-1] Symbol: V The above equation gives the electric potential at a distance r from the source charge Q. If this charge is negative, the electric potential is negative and given by V = -Q/(4πεor) Work and Electric Potential Suppose a unit charge is moved from point A to B such that B is closer to the source charge than A. Let rA and rB represent the distances of A and B from Q. Then, rA> rB. The potential difference between two points, A and B, can be written as ΔV = VB – VA = (Q/4πεo)(1/rB – 1/rA) Work is done against the electric field to move the unit charge from A to B. The work done is the negative change in electric potential. W = – ΔV The work done is negative because the displacement is opposite to the electric field. In other words, the charge is displaced in a direction opposite to the electric field. The electric potential at a point is said to be one volt if one joule of work moves one Coulomb of the electric charge against the electric field. Zero Potential The zero potential is a reference point from which electric potential values are measured. For a point charge, it is clear from the above equation that the electric potential is zero at infinity. This point is taken as a reference point. Hence, work done is the change in electric potential when a unit charge is brought from infinity to a point under consideration. Alternatively, the electric potential at a point is the work done in moving a unit charge from infinity to that point. The fundamental difference between electric potential energy and electric potential is that the former is the energy required to move an electric charge against an electric field. On the other hand, the latter is the work done in moving a unit charge from infinity to the point under consideration. Solution: Given q1 = 2 nC q2 = 3 nC r = 2 cm = 0.02 m The electric potential energy is given by U = kq1q2/r Or, U = (9 x 109 Nm2C-2 x 2 x 10-9 C x 2 x 10-9 C)/0.02 m Or, U = 2.7 x 10-6J Problem 2: A +2 μC test charge is initially at rest a distance of 15 cm from a +7 μC source charge fixed at the origin. The Coulomb force pushes the test charge away from the source charge, reaching 20 cm. What is the work done by the electric field? Solution: Given q1 = +2 μC q2= +7 μC rA = 15 cm = 0.15 m rB = 20 cm = 0.20 m The work done is given by W = -ΔV Or, W = -(kq1q2)(1/rB – 1/rA) Or, W = -(9 x 109 Nm2C-2 x 7 x 10-6 C x 2 x 10-6 C)(1/0.20 m- 1/0.15 m) Or, W = 0.21 J Problem 2: Two charges of magnitude 2 nC and 3 nC are placed at 2 cm from each other. Calculate the electric potential energy between these two charges. Solution: Given q1 = 2 nC q2 = 3 nC r = 2 cm = 0.02 m The electric potential energy is given by U = kq1q2/r Or, U = (9 x 109 Nm2C-2 x 2 x 10-9 C x 2 x 10-9 C)/0.02 m Or, U = 2.7 x 10-6J