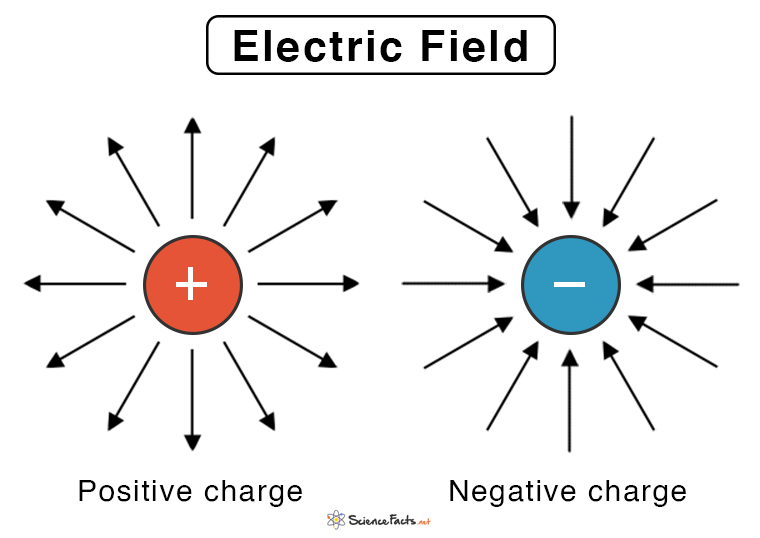
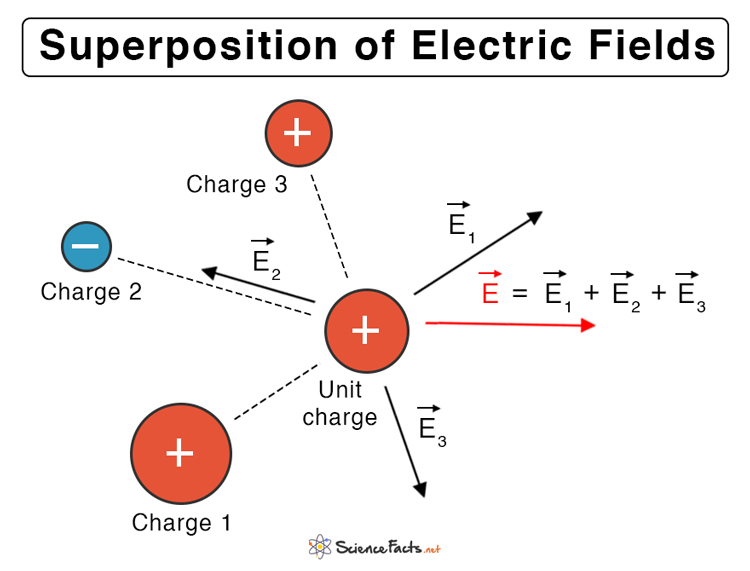
Electric Field Lines and Direction
Electric Field Flux
Electric Field Equation
Superposition of Electric Fields
Types of Electric Field
Work Done by an Electric Field
Examples and Problems
If the electric field and area vector makes an angle θ, then the equation is given by Magnitude of Electric Field The corresponding scalar equation gives the magnitude formula. Where, E: Electric field F: Electric force q: Electric charge SI Unit: Volt/meter (V/m) or Newtons/Coulomb (N/C) Dimensional Formula: [M L T-3 I-1]
How to Find Electric Field for a Point Charge
- Coulomb’s Law The electric field can be calculated using Coulomb’s Law. According to this law, the electric force between two point charges is directly proportional to the product of the charge and inversely proportional to the square of the distance between them. Where, q1, q2: Magnitudes of the two charges r: Distance of separation between the charges εo: Permittivity of free space (= 8.85 x 10-12 C2N-1m-2 or epsilon naught value) By definition, the electric field is the force per unit charge. Therefore, q1 = q and q2 = 1. Then, the electric field is given by the following equation. Thus, the strength of an electric field depends on the magnitude of the source charge.
- Gauss’s Law The electric field can be calculated by another method. Gauss’s Law is applied to find the electric field at any point on a closed surface. According to this law, the electric flux through any closed surface is proportional to the total electric charge enclosed by this surface. Mathematically, the law states that the electric flux is the integral of the dot product between the electric field and an infinitesimal surface area. Using Gauss’s Law, the electric field can be calculated for the following cases:
SphereCylinderCurrent-carrying Wire or Line ChargeCircular Disc and RingInfinite Plane/SheetParallel Plate CapacitorElectric DipoleCoaxial Cable
Where
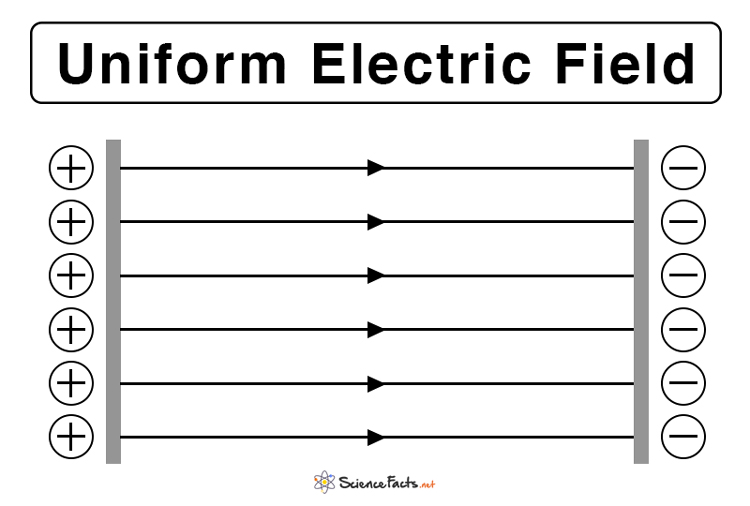
1. Uniform Electric Field
The electric field is said to be uniform if its value remains constant over a region in space. Its magnitude does not depend on the displacement, and the field lines are parallel and equally spaced. Example: A uniform electric field can be created between two charged parallel plates, also known as a capacitor. The electric field lines come out of the positive plate and terminate in the negative plate.
2. Non-uniform Electric Field
The electric field is non-uniform if its value does not remain constant over a region in space. In this case, the electric field lines are not parallel. Example: The field generated by a point charge is radial, and its strength is inversely proportional to the distance. By definition, work done is the dot product of the force and displacement. The work done by a uniform electric field E in moving a charge q through a distance d is given by, If the field and the displacement are in the same direction, then And The quantity ΔV is known as the potential difference or voltage. It gives the change in potential energy when a unit charge moves from one position to another in the presence of an electric field. Therefore, the work done by an electric field is
How to Find the Work Done by the Electric Field Due to a Point Charge
The electric potential due to a point charge q is given by, Suppose a charge moves from a position that is at a distance r1 from the source charge to a distance r2. Then, the change in potential energy, which is the work done, is given by Solution: Given, F = 8 N q = 3 μC Therefore, E = F/q = 8 N/3 μC = 2.67 x 106 N/μC Problem 2. A small charge, q = 4 mC, is found in a uniform electric field E = 3.6 N/C. What is the force on the charge? Solution: Given, q = 4 mC E = 3.6 N/C F = qE = 4 mC x 3.6 N/C = 14.4 mN