Examples
How to Calculate Elastic Potential Energy
Elastic Potential Energy in 3D
Problems and Solutions
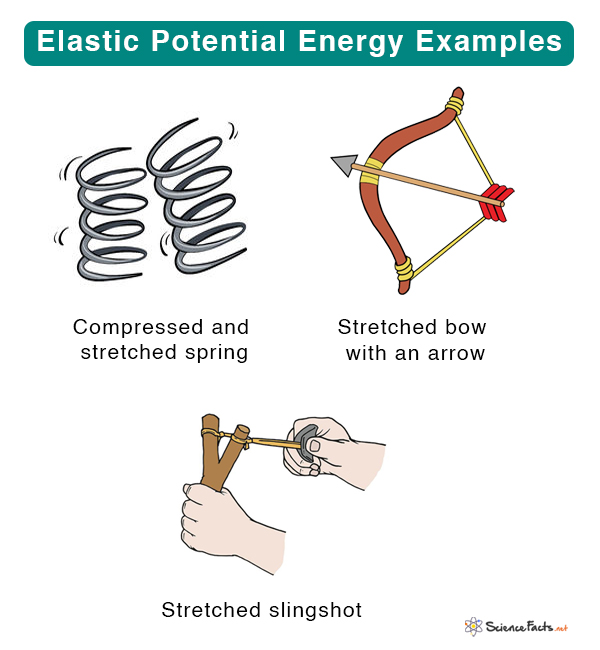
The spring of a wind-up clockThe stretched bow of an archerA bent diving board just before a diver takes a diveThe rubber band of a stretched slingshotWhen a bouncy ball hits the wall or floor
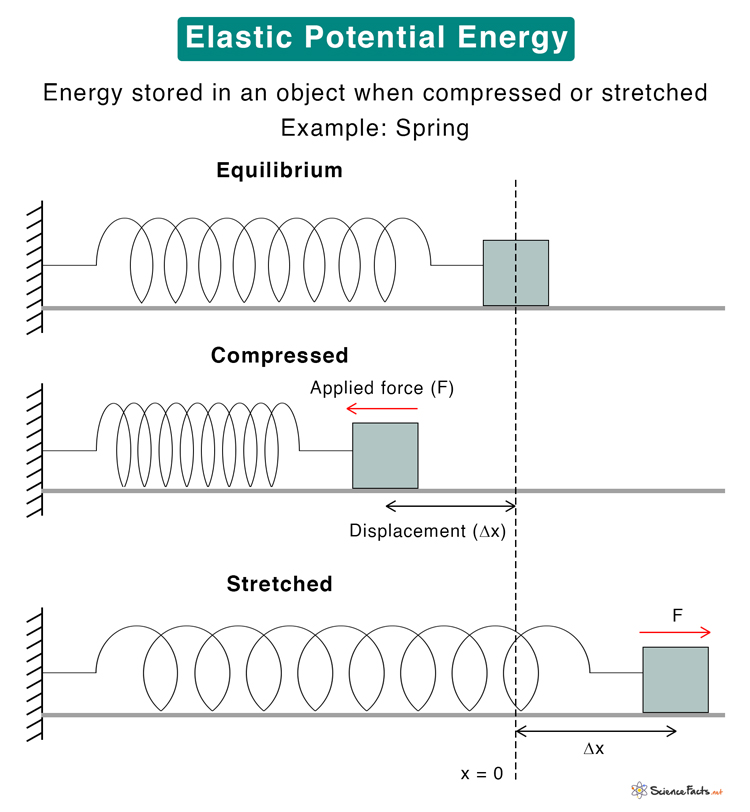
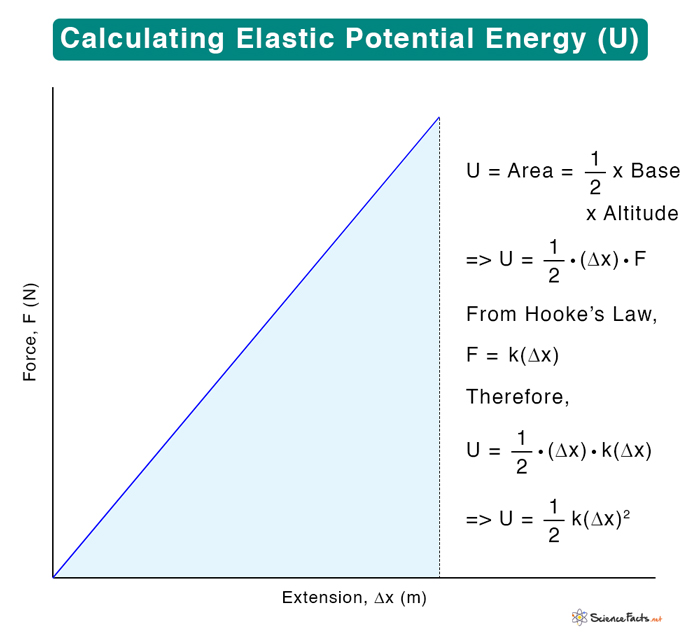
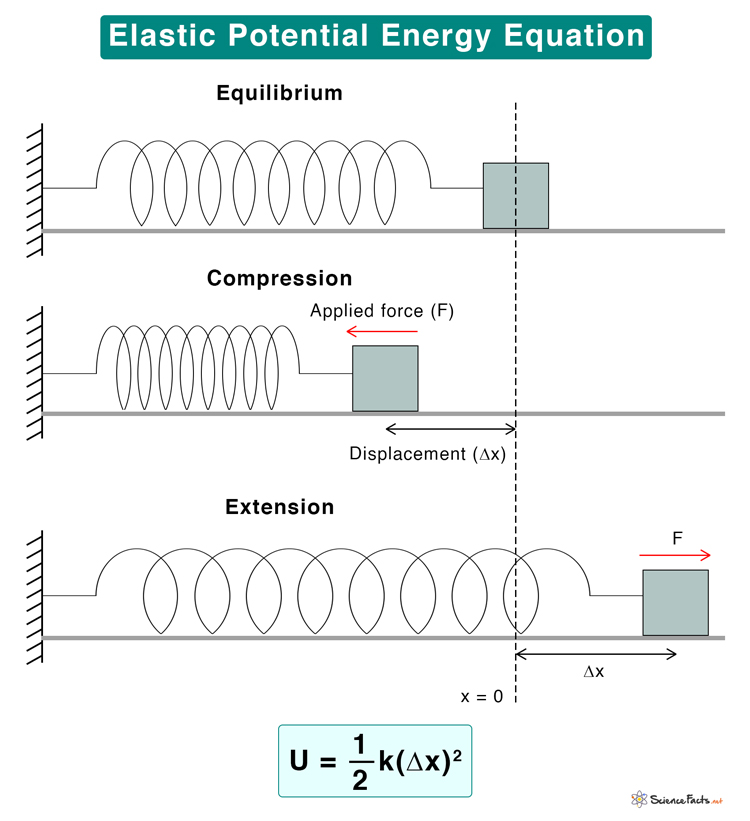
Where, F: Applied force Δx: Deformation k: Spring constant The constant of proportionality is known as the spring constant. Its unit is Newton per meter or Nm-1. The deformation can be extension or compression. In either case, energy is stored. Spring energy is an example of elastic potential energy. The force vs. extension graph of spring is shown below. The graph is linear. The area under the graph gives the work done in stretching the spring. Since work is done at the expense of energy, this area also gives elastic potential energy. We know that the area of a triangle is Therefore, the elastic potential energy, U, can be calculated as follows: Unit: Joule or J Dimension: [ML2T-2] Where σ is the stress, ε is the strain, and V is the volume. The above equation is the elastic energy density. Solution: Given U = 15 J k = 175 N/m The elastic potential energy is given by U = ½ k (Δx)2 Or, (Δx)2= 2U/k Or, Δx= sqrt (2U/k) Or, Δx= sqrt (2 x 15J/175 Nm-1) Or, Δx= 0.17 m