A lens with one of its sides converging and the other diverging is known as a meniscus lens. A double concave lens is diverging on both of its refracting surfaces. Whereas, if one side has no curvature but the other side is concave, it is known as a plano-concave lens.
Is Concave Lens a Diverging Lens?
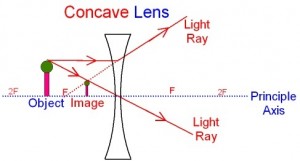
Ray Diagram Showing Image Formation by Diverging Lens
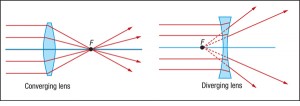
Converging vs. Diverging Lens
Diverging Lens Equations
Diverging Lens Ray Tracing Video
Animation: Diverging Lens Object-Image Relations
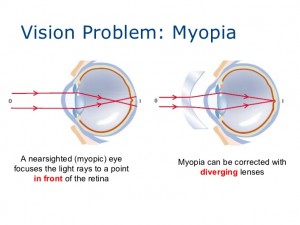
Applications
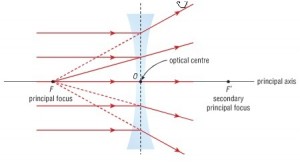
Any ray of light that is parallel to the principal axis of the lens will pass through its focal point after refraction. Any incident ray of light that passes through the focus of the lens before getting refracted will emerge parallel to the principal axis on refraction. A ray of light that is incident on the optical center of the lens will pass through undeviated.
For all positions of the object, the image is erect, smaller in size than the object and formed within the focal length of the lens. While drawing a ray diagram, it is essential to consider at least two principal rays emanating from the top of an extended object. While one of them should remain parallel to the principal axis, another one should pass through the optical center of the lens. Other than the basic structural variations between concave mirrors and diverging lenses, the main difference lies in the fact that the former works by the principle of reflection while the latter utilizes that of refraction. Needless to mention, the image formation procedure is completely distinct for the two.
The focal length of a thick lens in air can be calculated by the lensmaker’s equation, ] where f is the focal length of the lens, n is the refractive index of the material that makes up the lens, R1 is the radius of curvature of the lens surface closest to the object, R2 is the radius of the lens surface farthest from the object and d is the thickness of the lens. f is positive for a converging lens and negative for a diverging one. For a thin lens placed in air, d ≈ 0. Hence, the lensmaker’s formula takes the form,
The reciprocal of the focal length is known as the optical power of the lens. If the focal length is expressed in meters, then the said quantity determines the optical power in dioptres. The magnification equation relates the object and image distances with the object height (ho) and image height (hi). According to it, the magnification M produced by a lens is given by, M = Refracting telescopes generally use a convex-concave lens combination to enable magnified viewing of far away objects. The study of the diverging lens has advanced the Optics branch of Physics in a multitude of ways. While it provides an interesting opportunity to learners for grasping the basic characteristics of lenses, it finds ample use in the field of medical science and astronomy as well. https://www.physicsclassroom.com/class/refrn/Lesson-5/Diverging-Lenses-Ray-Diagrams https://www.physicsclassroom.com/class/refrn/Lesson-5/Diverging-Lenses-Object-Image-Relations http://hyperphysics.phy-astr.gsu.edu/hbase/geoopt/raydiag.html