This concept was introduced by French physicist Louis de Broglie in his doctoral thesis in 1924, revolutionizing our understanding of the nature of matter.
de Broglie Equation
de Broglie Wavelength of Electron
Thermal de Broglie Wavelength
1. Planck’s Constant (h)
Central to this equation is Planck’s constant, denoted as “h.” Planck’s constant is a fundamental constant of nature, representing the smallest discrete unit of energy in quantum physics. Its value is approximately 6.626 x 10-34 Jˑs. Planck’s constant relates the momentum of a particle to its corresponding wavelength, bridging the gap between classical and quantum physics.
2. Particle Momentum (p)
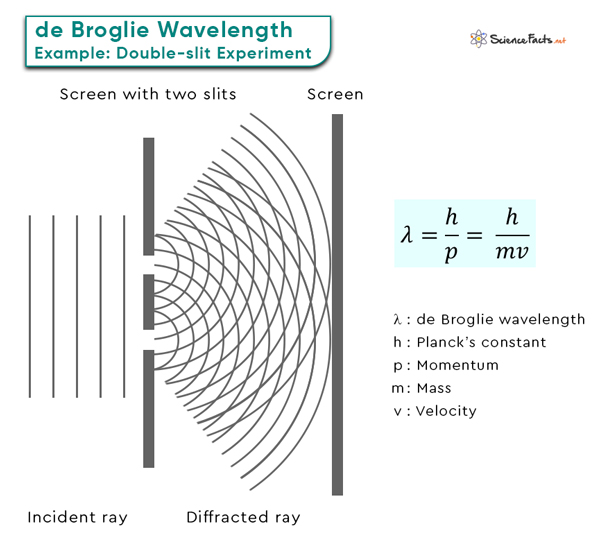
The second critical component of the equation is the particle’s momentum, denoted as “p”. Momentum is a fundamental property of particles in classical physics, defined as the product of an object’s mass (m) and its velocity (v). In quantum mechanics, however, momentum takes on a slightly different form. It is the product of the particle’s mass and its velocity, adjusted by the de Broglie wavelength. The mathematical formulation of de Broglie wavelength is We can replace the momentum by p = mv to obtain Unit The SI unit of wavelength is meter or m. Another commonly used unit is nanometer or nm. This equation tells us that the wavelength of a particle is inversely proportional to its mass and velocity. In other words, as the mass of a particle increases or its velocity decreases, its de Broglie wavelength becomes shorter, and it behaves more like a classical particle. Conversely, as the mass decreases or velocity increases, the wavelength becomes longer, and the particle exhibits wave-like behavior. To grasp the significance of this equation, let us consider the example of an electron. Consider an electron moving at 2 x 106 m/s. The rest mass of an electron is 9.1 x 10-31 kg. Therefore, These short wavelengths are in the range of the sizes of atoms and molecules, which explains why electrons can exhibit wave-like interference patterns when interacting with matter, a phenomenon famously observed in the double-slit experiment. At finite temperatures, particles within a system possess a range of energies described by the Maxwell-Boltzmann distribution. Some particles have relatively high energies, while others have low energies. The thermal de Broglie wavelength accounts for this distribution of kinetic energies. It helps to understand the statistical behavior of particles within a thermal ensemble.
Mathematical Expression
The thermal de Broglie wavelength (λth) is determined by incorporating both the mass (m) of the particle and its thermal kinetic energy (kT) into the de Broglie wavelength equation: Here, k is the Boltzmann constant, and T is the temperature in Kelvin.