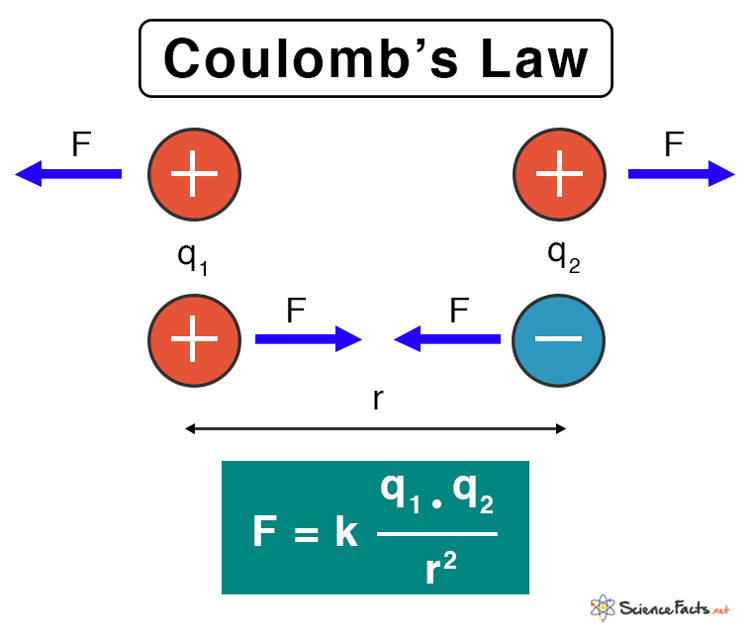
Statement of Coulomb’s Law Coulomb’s law states that the electrostatic force between the two particles is
Directly proportional to the product of the magnitude of the chargesInversely proportional to the square of the distance between the two charges
This law is named after French physicist Charles-Augustin de Coulomb, who published it in 1785.
Coulomb’s Law Equation
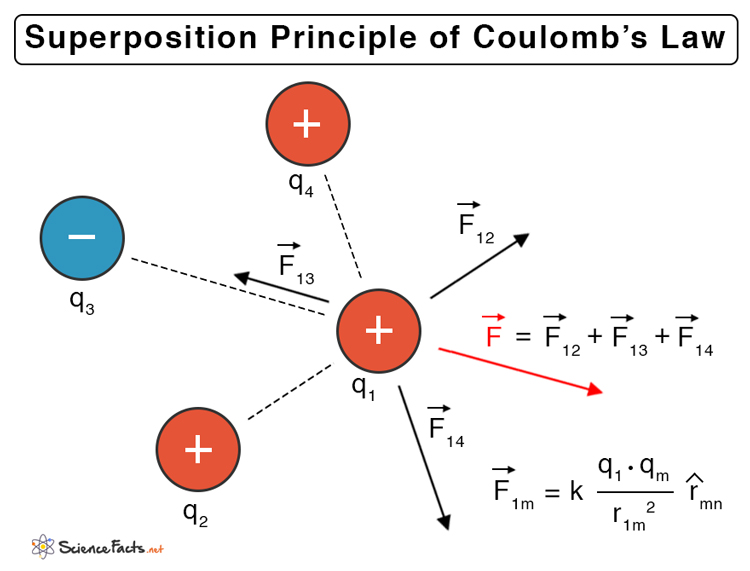
Superposition Principle of Coulomb’s Law
Limitations
Applications
Examples and Practice Problems
Suppose two point charges are separated by a certain distance. Then, according to Coulomb’s law, the electrostatic force, also known as Coulomb’s force, between the two charges is given by the following formula. Where, F: Electrostatic force k: Coulomb’s constant q1, q2: Magnitude of the point charges r: Distance of separation between the charges SI Unit: Newton or N Dimension: [M L T-2] Because of the inverse relationship, this law is sometimes called Coulomb’s inverse square law. Vector Form The vector form of Coulomb’s law is given by, Where,
Coulomb’s Law Constant
The constant in Coulomb’s law is known as Coulomb’s constant, which is denoted by k. Suppose, q1 = 1, q2 = 1, and r = 1, then, Therefore, Coulomb’s constant is defined as the electrostatic force experienced by two unit charges when a unit distance separates them. It is expressed as follows. In free space, In a medium, Where, εo: Permittivity of free space or vacuum (= 8.85 x 10-12 C2N-1m-2) εr: Permittivity of the medium The ratio of εr and εo is known as the relative permittivity of the medium or dielectric constant. Dielectric Constant: κ = εr/εo Putting the value of εo gives the value of k, Coulomb’s Constant: 9 x 109 Nm2C-2 Using the expression for k, the Coulomb’s Law equation in free space is given by, According to the superposition of forces, all linear forces can be added vectorially. The net force is the vectorial sum of all the individual forces. Consider a system of n charges given by q1, q2, …, qn, the force due to charges q1 and q2 is, Where, Similarly, the force between q1 and any other charges are, Therefore, the net force due to q1 is, Solution: Given, q1 = 6.25 nC q2 = 6.25 nC r = 42 cm = 0.42m We have, F = k q1 q2 /r2 = (9 x 109 Nm2C-2 x 6.25 nC x 6.25 nC)/0.422 m2 = 2 μN Problem 2. The force between two identical charges separated by 2 cm is equal to 45 N. What is the magnitude of the two charges? Solution: Given, F = 45 N d = 2 cm = 0.02 m q = q1 = q2 We have, F = k q1 q2 /r2 = k q2/r2 Or, q = sqrt (F r2/k) = sqrt (45 N x (0.02 m)2/ 9 x 109 Nm2C-2) = 1.41 μC Problem 3. Two balloons with charges of +4 µC and -8 µC attract each other with a force of 0.0625 N. Determine the separation distance between the two balloons. Solution: Given, F = 0.0625 N q1 = 4 μC = 4 x 10-6 C |q2|= 8 μC = 8 x 10-6 C We have, F = k q1 q2 /r2 Or, r = sqrt (k q1 q2 / F) = sqrt (9 x 109 Nm2C-2 x 4 x 10-6 C x 8 x 10-6 C/0.0625 N) = 2.15 m Problem 4. Two neutrally charged bodies are separated by 0.5 cm. Electrons are stripped off from one body and placed on the second body until a force of 2 μN is generated between them. How many electrons were transferred between the bodies? Solution. Given, q1 = +ne q2 = -ne e = 1.6 x 10-19 C r = 0.5 cm = 5 x 10 -3 m F = 2 μN = 2 x 10-6 N We have, F = k q1 q2 /r2 Or,|F| = k n2e2 /r2 Or, n = sqrt (F r2 / k e2) = sqrt (2 x 10-6 N x (5 x 10 -3 m)2 / (9 x 109 Nm2C-2 / (1.6 x 10-19 C)2)) = 6.5 x 108