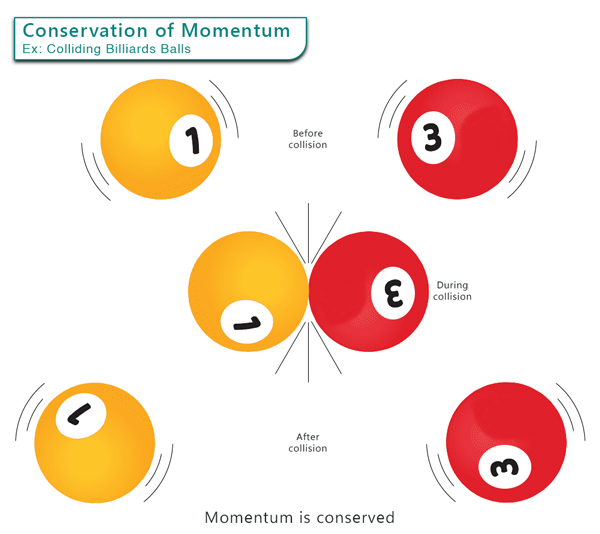
The conservation of angular momentum is a fundamental concept of Physics to study objects in motion. The law of conservation of momentum states that “the total momentum of an isolated (closed) system is conserved as long as no external forces are acting on it.” By isolated system, we mean no matter is exchanged between the system and the surroundings. The conservation of momentum is most closely related to Newton’s third law. Mathematically, momentum is equal to an object’s mass multiplied by its velocity. It is a vector quantity having both magnitude and direction. Momentum can neither be created nor destroyed. It is conserved in all three directions in space. For example, when gas molecules collide, momentum is conserved along the x, y, and z directions. Momentum conservation law applies to both linear momentum and angular momentum. Its application extends from understanding everyday collisions to exploring the dynamics of astronomical objects.
Examples
Equation
Conservation of Momentum and Collisions
Problems and Solutions
Linear Momentum: When a rocket is launched into space, it starts with a net zero momentum. During its journey, the downward momentum of the burning fuel is equal to the upward momentum of the rocket. Therefore, the net momentum of the rocket-propulsion system remains zero.Angular Momentum: A skater slowly rotates when spreading her arms. However, when she drops her arms, she rotates faster. The product of angular velocity and radius gives the angular momentum. When the skater spreads her arms, the radius is longer, and the angular velocity is lower. When she pulls her arms, the radius is smaller, and the angular velocity is higher. In both cases, the angular momentum remains unchanged and is conserved.
Recall that momentum is the product of mass and velocity. If m1, m2, …, mn represents the masses, v1i, v2i, …, vni represent the initial velocities, and v1f, v2f, …, vnf represent the final velocities, the above expression reduces to The above expression for momentum conservation applies to one dimension only. For three-dimensional representation, we use vectors. To summarize,
Elastic collision – both momentum and kinetic energy are conserved Inelastic collision – only momentum is conserved, not kinetic energy
In addition, there are perfectly inelastic collisions, where objects stick together after the collision, and only momentum is conserved. Solution Given, mA = 1000 kg, vAi = 20 m/s, mB = 1200 kg, and vBi = 15 m/s The velocity of car A is vAf = (mA – mB)/(mA + mB) vAi + 2mB/(mA + mB) vBi => vAf = (1000 kg – 1200 kg)/(1000 kg + 1200 kg) x 20 m/s + 2 x 1000 kg/(1000 kg + 1200 kg) x 15 m/s => vAf = 11.8 m/s The velocity of car B is given by vBf = 2mA/(mA + mB) vAi – (mA – mB)/(mA + mB) vBi => vBf = 2 x 1000 kg/(1000 kg + 1200 kg) x 20 m/s – (1000 kg – 1200 kg)/(1000 kg + 1200 kg) x 15 m/s => vBf = 19.54 m/s Both cars travel right after the collision. Problem 2: A billiard ball with a mass of 0.2 kg is moving at a velocity of 3 m/s to the right. It collides with another stationary billiard ball of the same mass. Determine the velocities of both balls after the collision. Solution Given, mA = 0.2 kg, vAi = 3 m/s, mB = 0.2 kg, and vBi = 0 m/s When two similar masses collide, they exchange velocities. Therefore, the first ball will come to rest, and the velocity of the second ball is 3 m/s. Problem 3: A rocket of mass 5000 kg is initially at rest on the launchpad. The exhaust gases are expelled from the rocket with a velocity of 1000 m/s relative to the rocket. If the mass of the expelled gases is 100 kg, what is the rocket’s velocity after the gases are expelled? Solution Given mrocket = 5000 kg, vrocket, initial = 0, mgas = 100 kg, vgas, initial = 0 and vgas, final = 1000 m/s From the law of conservation of momentum mrocket x vrocket, initial + mgas x vgas, initial = mrocket x vrocket, final + mgas x vgas, final => 5000 kg x 0 + 100 kg x 0 = 5000 kg x vrocket, final – 100 kg x 1000 m/s => 0 = 5000 kg x vrocket, final – 100000 kg ˑ m/s => vrocket, final = 20 m/s Problem 4: A hunter fires a rifle with a mass of 3 kg. The bullet, with a mass of 0.05 kg, is expelled from the rifle with a velocity of 400 m/s. Determine the recoil velocity of the rifle. Solution Given mrifle = 3 kg, vrifle, initial = 0, mbullet = 0.05 kg, mbullet, initial = 0 m/s, vbullet, final = 400 m/s From the law of conservation of momentum mrifle x vrifle, initial + mbullet x vbullet, initial = mrifle x vrifle, final + mbullet x vbullet, final => 3 kg x 0 + 0.05 kg x 0 = 3 kg x vrifle, final – 0.05 kg x 400 m/s => 0 = 3 kg x vrifle, final – 20 kg m/s => vrifle = 6.67 m/s