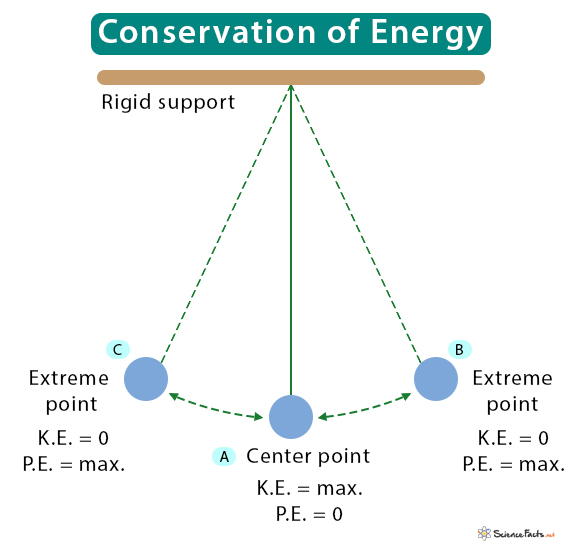
As a result of energy conservation, the total energy in an isolated system is constant. If there is a loss of energy in one part of an isolated system, there must be a gain in another part.
Examples
Equation
The stored potential energy is converted into kinetic energy when the pendulum returns to the center. At the center, the potential energy is zero, and the kinetic energy is maximum. Therefore, at any time, the sum of the two is constant. Since the sum of kinetic and potential energy gives mechanical energy, a swinging pendulum is an example of the conservation of mechanical energy.
ii. Sliding Block
When a block slides down a ramp, its potential energy is converted into kinetic energy. However, due to friction, some energy is lost as heat. At any point, the sum of potential energy, kinetic energy, and thermal energy due to friction remains constant. The block and the ramp as a whole constitute an isolated system.
2. Conservation of Kinetic Energy
Collision between Objects
During a collision between two bodies, the sum of kinetic energy before collision equals the sum after the collision.
3. Conservation of Chemical Energy
i. Dynamite Explosion
When a stick of dynamite explodes, the chemical energy present in the explosive is converted into kinetic energy, heat, sound, and light. The sum of all four energy forms is equal to chemical energy.
ii. Combustion of Fuel
In a combustion reaction, fuel burns in the presence of oxygen to produce sound and heat. Thus, all the chemical energy present in the fuel is converted into kinetic energy, heat energy, and sound energy. If we add the three energies, the sum equals the fuel’s chemical energy.
4. Conservation of Thermal Energy
Digestion of Food
The quantity of heat obtained by consuming food during the daily food intake of an animal equals the daily amount of energy released by the animal in the forms of work done, heat generated, and energy in the waste products. We assume that the animal is not gaining or losing any weight. Consider a system that takes in heat and does valuable work. For this system, the energy conservation equation is given by UT = Ui + Q + W Where UT: Total energy of the system Ui: Internal energy of the system Q: Heat added to or removed from the system W: Work done by or on the system Einstein’s Mass-Energy Equation Noted physicist Albert Einstein discovered in the early 20th century that mass could be converted into energy, known as mass-energy equivalence. The amount of energy associated with a specific amount of mass is given by the following famous equation in physics. E = mc2 Where, E: Energy M: Mass c: Speed of light (=3 x 108 m/s)