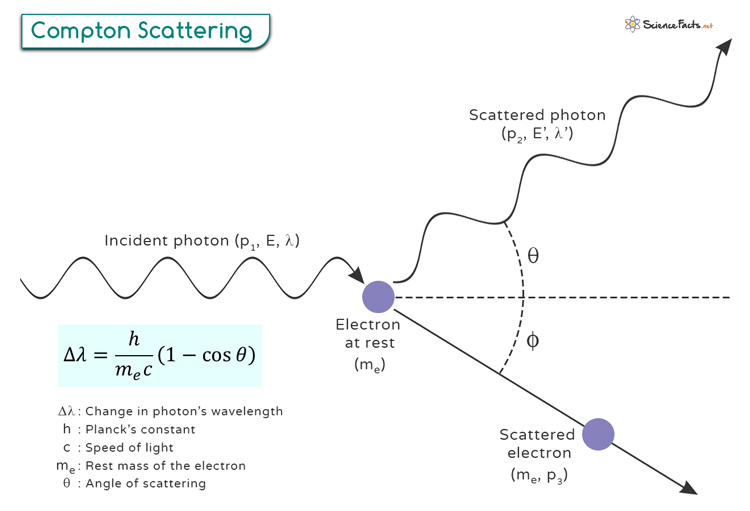
Compton scattering played a crucial role in confirming the particle nature of light. This process was first explained by American physicist Arthur Holly Compton in 1923, who demonstrated that light behaves as both particles (photons) and waves.
Equation
Derivation
Applications
Inverse Compton Scattering
Compton Effect vs. Photoelectric Effect
The equation is written as: Where: Δλ is the change in wavelength of the photon λ’ is the wavelength of the scattered photon λ is the wavelength of the incident photon h is Planck’s constant me is the rest mass of the electron c is the speed of light The scattering angle θ represents the angle between the incident and the scattered photon’s direction. This equation demonstrates that a shift in wavelength occurs due to the interaction between the photon and electron. p1 and E are the photon’s initial momentum and energy, respectively. p2 and E’ are the photon’s final momentum and energy, respectively. me and p3 are the electron’s rest mass and final momentum, respectively. θ is the angle by which the photon scatters. φ is the angle by which the electron recoils. We assume that the photon initially moves along the x-direction so that only the x and the y components of the momentum will be considered in our derivation. Conservation of momentum along the x- and y- directions gives rise to the following equations. p1 = p2 cos θ + p3 cos φ (x-direction) p2 sin θ = p3 sin φ (y-direction) According to the conservation of energy, the total energy before the interaction is given by E + mec2. After the scattering, the photon loses energy and momentum while the electron gains the same. Conservation of energy gives us the following relativistic equation. We aim to solve for E’ in terms of cos θ and eliminate φ in the process. Continuing from the energy equation, we get Squaring both sides We need to replace p3 and use the momentum conservation equations. (p3 cos φ)2 = (p1 – p2 cos θ)2 (p3 sin φ)2 = (p2 sin θ)2 Adding the two equations, we get p32 = p12 + p22 – 2 p1p2 cos θ Back to the energy equation Using the photon-energy equation E = pc, we can rewrite the energy equation as Using the relationship between energy and momentum for a photon, E = hc/λ, where h is Planck’s constant and λ is the wavelength, we can rewrite the equation as Which is the Compton wavelength shift equation for the photon. The minimum change in wavelength occurs when θ = 0° or cos θ = 1, resulting in Δλ = 0. The maximum change in wavelength occurs when θ = 180° or cos θ = -1, resulting in Δλ = 2h/mec. In this case, the photon transfers to the electron as much momentum as possible. The value of this maximum change is The quantity h/mec is known as the Compton wavelength of the electron and is equal to 2.43 x 10-12 m.