What is the Direction of the Centripetal Force
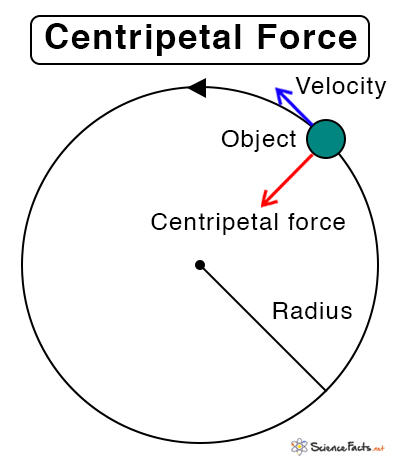
The centripetal force is directed towards the center of curvature of the curved path traced by the object. It is at a right angle to the object’s motion and causes the object to change its direction.
How Does the Centripetal Force Affect Circular Motion
In a circular motion, the centripetal force is along the radius toward the center.
Examples and Applications of Centripetal Force
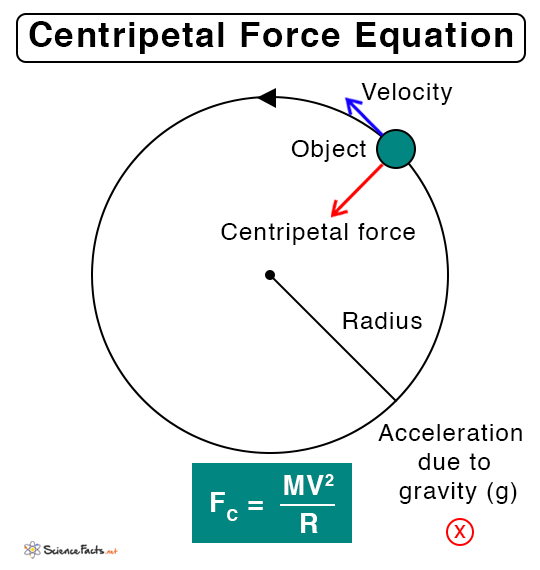
Centripetal Force Equation
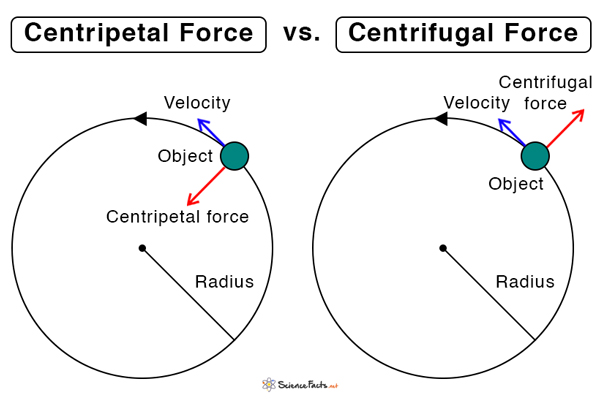
Difference Between Centripetal and Centrifugal Force
Example Problems
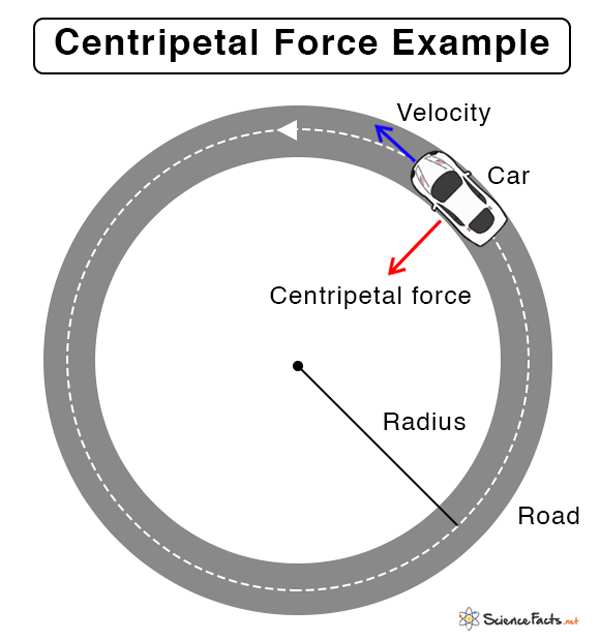
The force experienced by a car when it makes a turn on a circular road, as shown belowThe Earth’s gravitational force keeps satellites in orbit and causes centripetal motionThe Earth’s gravity is responsible for keeping objects on the surfaceThe tension force on a string swirling a bucket of waterThe force experienced by a roller coaster in an amusement park when going around a loopThe force experienced by a pendulum while swinging
F = ma Linear and Angular Velocity The angular velocity of an object in a circular motion is defined as the rate at which it turns around its path. Suppose the object describes an angle θ in time t, then the angular velocity ω is given by ω = θ/t The relationship between the angular velocity ω and linear velocity v is given by v = ωr Here, r is the radius of the circular path. Centripetal Acceleration An object moving in a circular path experiences acceleration known as centripetal acceleration. This acceleration is directed radially inward and is given by a = ω2r = v2/r Therefore, the magnitude of the centripetal force is given by FC = mv2/r Unit: Newton or N Dimension: MLT-2 Work Done by Centripetal Force The object moves in a circle of constant radius. The centripetal force is always directed toward the center. In this case, the force and the displacement vectors are at right angles. Therefore, the work done by the centripetal force is zero.
Centripetal Force vs. Centrifugal Force
Soln.: Given, m = 1200 kg r = 600 m v = 20 m/s FC = mv2/r = 1200 kg x (20 ms-1)2 / 600 m = 800 N P.2. An object of mass 20 kg is in a circular orbit of radius 20 m at a velocity of 20 m/s. Calculate the centripetal force required to maintain this orbit. Soln.: Given, m = 20 kg r = 20 m v = 20 m/s FC = mv2/r = 20 kg x (20 ms-1)2 / 20 m = 400 N