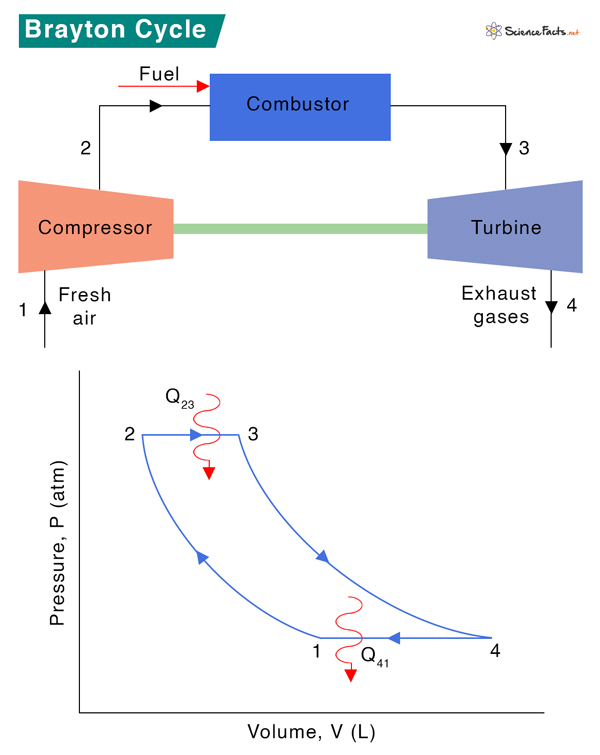
Brayton cycle is named after American engineer George Brayton, who developed and patented a constant pressure engine in 1872. It formed the basis of the gas turbine engine.
Theory
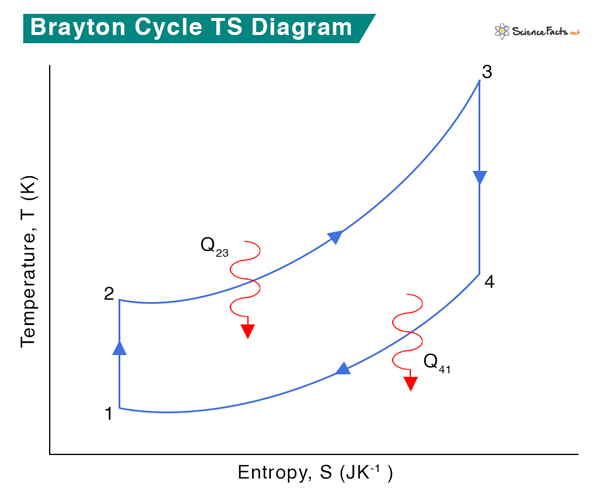
PV and TS Diagrams
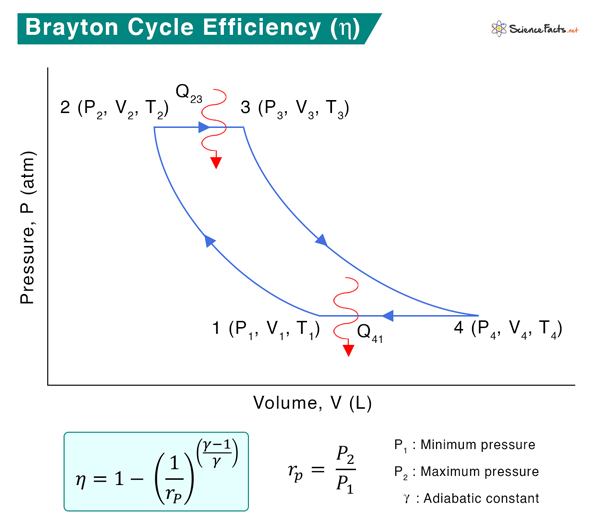
Thermal Efficiency
Process 1 → 2: Isentropic Compression Fresh ambient air is drawn into the compressor and compressed from pressure P1 to P2. The volume reduces from V1 and V2, and the temperature increases from T1 to T2. The entropy, S, remains constant: S1 = S2. Process 2 → 3: Heat Addition Fuel and compressed air are sent to the combustor, where fuel burns at constant pressure, P2 = P3. Heat is added to the compressor. The temperature rises from T2 to T3, volume expands from V2 to V3, and entropy increases from S2 to S3. Process 3 → 4 Isentropic Expansion The heated and compressed gas expands adiabatically through a turbine. The gas works on the turbine’s blades and loses its internal energy, which is equivalent to work that leaves the system. The pressure decreases from P3 to P4, temperature decreases from T3 to T4, and volume slightly increases from V3 to V4. The process is isentropic, which means S3 = S4. Process 4 → 1 Heat Rejection Isobaric heat rejection occurs in this process at constant pressure, P4 = P1. A slight decrease in volume from V4 to V1 occurs due to heat rejection. Since it is a heat rejection process, the gas temperature decreases from T4 to T1, and entropy reduces from S4 to S1. Heat is added to during the constant-pressure process 2 → 3 and is given by Q23 = CP (T3 – T2) Heat is rejected during the constant-pressure process 4 → 1 and is given by Q41 = CP (T1 – T4) Where Cp is the specific heat at constant pressure. According to the first law of thermodynamics, the net change in internal energy is zero for a closed circle. Δu = 0 => (Q12 – W12) + (Q23 – W23) + (Q34 – W34) + (Q41 – W41) = 0 Q12 = Q34 = 0 (since they are adiabatic processes) Therefore, Q23 + Q41 – (W12 + W23 + W34 + W41) = 0 => Q23 + Q41 – W = 0 => W = Q23 + Q41 Where W = W12 + W23 + W34 + W41 is the net work done. Therefore, Adiabatic gas equations give Where γ is the adiabatic constant. Since P2 = P3 and P4 = P1 The efficiency equation is reduced to Here, T1 is the initial temperature of the undisturbed gas, T2 is the initial temperature before the combustion, T3 is the final temperature of the combustion process, and T4 is the temperature of the gas after it leaves the turbine. The smaller the T1/T2 ratio, the higher the efficiency. Therefore, if more heat is added and less heat is lost during the engine operation, the thermal efficiency of the Brayton cycle will be high. Rewriting the above equation as ( \frac{P_2}{P_1} ) is called the pressure ratio during compression and is denoted by rP. Therefore, The pressure ratio in most modern engines ranges from 11 to 16.