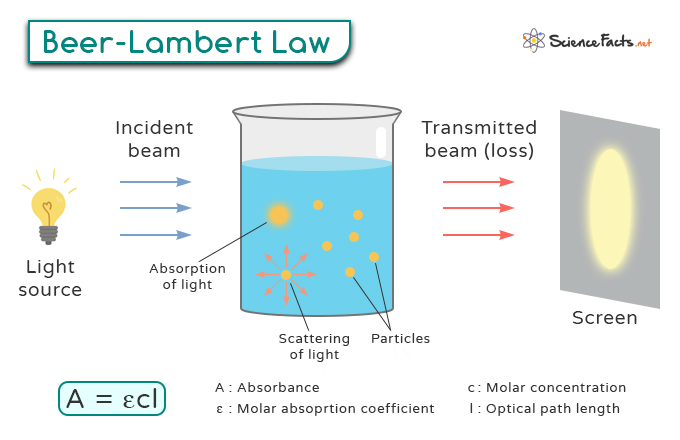
Statement: “The amount of light absorbed by a substance is directly proportional to the substance’s concentration and the path length of light.”
Equation
Derivation
- Determining the Intensity According to Beer-Lambert Law, we can express this relationship mathematically as: Where: – A represents absorbance – ε (epsilon) is molar absorptivity – c signifies concentration – l denotes path length Absorbance (A) refers to the amount of light absorbed by a sample as it passes through it. It is a dimensionless quantity that is calculated based on the intensity of the incident light (Io) and the transmitted light (I) using the following relationship: Measuring absorbance involves comparing light intensity before and after interacting with a sample. It is typically done using a spectrophotometer, which emits light of a specific wavelength onto the sample. Molar absorptivity (ε), also known as molar absorption coefficient or molar extinction coefficient, measures how strongly a substance absorbs light at a specific wavelength. It can vary significantly depending on the wavelength of the incident light. A higher ε value means stronger absorption at that wavelength. The unit of molar absorptivity is liters per mole per centimeter (L mol-1 cm-1). The path length (l) is the physical distance that the light beam travels through the absorbing medium, typically measured in centimeters (cm). The longer the path length, the more opportunities there are for the light to interact with the sample molecules, leading to higher absorbance. Beer-Lambert Law is graphically represented as follows. When a beam of monochromatic light of initial intensity Io passes through a medium, it is partially absorbed by the medium. The decrease in light intensity is proportional to the intensity of the incident light and the path length l through the medium. Mathematically, this relationship is expressed as: where dI is the infinitesimal decrease in intensity, α is the absorption coefficient, and dx is the infinitesimal path length. To find the total absorption over a finite path length l, we integrate the above differential equation. Rearranging the terms, we get: Integrating the left-hand side from Io to I and the right-hand side from 0 to l: This simplifies to: Solving for I, we exponentiate both sides: This shows that light intensity decreases exponentially with the path length in the medium.
- Relation to Concentration The absorption coefficient α is proportional to the concentration of the absorbing species c in the medium and the molar absorptivity ε of the species, giving Substituting this into the exponential equation: To express the law in a more commonly used form, we take the natural logarithm: The left-hand side of the above equation is the absorbance A of the medium. Therefore, Thus, we derived the Beer-Lambert Law in its final form.
Applications
Limitations