Angular displacement is analogous to linear displacement. However, during linear displacement, the object moves in a linear path. On the other hand, during angular displacement, the object moves in a circular path.
Angular Displacement Equation
Example Problems
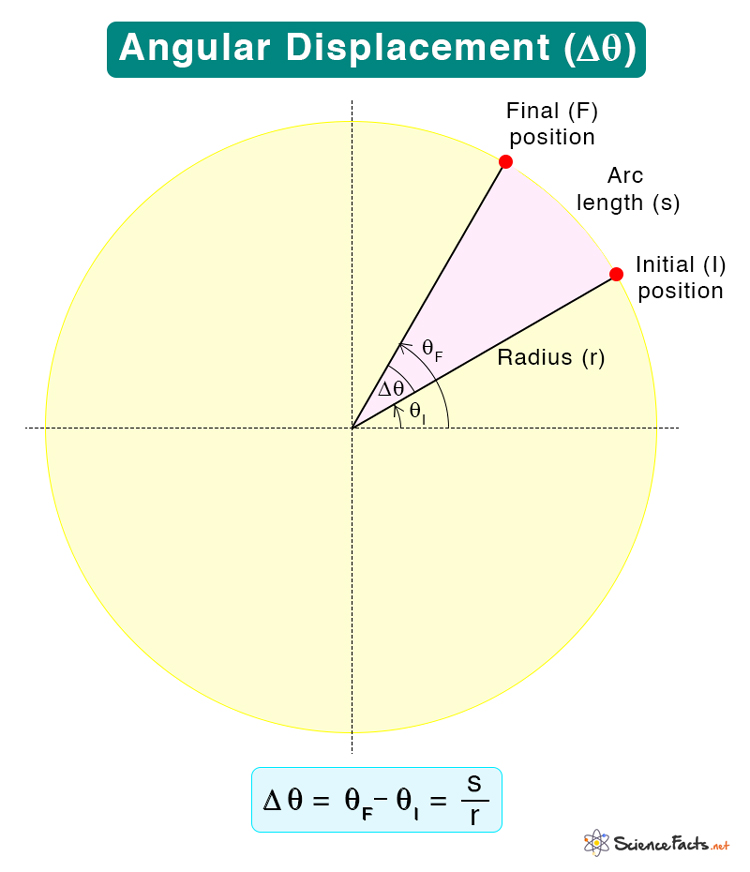
Δθ = θf – θi Where Δθ: Angular displacement θf: Final position of the object θi: Initial position of the object Symbol: Δθ (delta theta) or θ Unit: Degree or radian (1 radian = 57.3 degrees)
Angular Displacement From Linear Displacement
There is another way to calculate the angular displacement. Suppose s is the arc length and r is the object’s distance from its axis of rotation. r is also the radius of the circular path the object makes. The angular displacement is Angular displacement = arc length/radius of the circular path θ = s/r The arc length is almost equal to the linear displacement. Therefore, the above equation establishes a relationship between linear and angular displacements. It can be seen that the two are proportional to each other. If the linear displacement increases or decreases, the angular displacement will also increase or decrease. On the other hand, the angular displacement is inversely proportional to the radius. Suppose two objects with different radial distances rotate about a common axis with the same angular displacement. The object further from the axis will traverse a longer linear distance than the one closer.
Angular Displacement, Angular Velocity, and Angular Acceleration
The rate of change in angular displacement is called angular velocity. The rate of change of angular velocity is called angular acceleration. The angular displacement (θ), angular velocity (ω), and angular acceleration (α) are related by the following equation. θ = ωt + ½ αt2 Solution Given, diameter (d) = 9.5 m => r = d/2 = 9.5 m/2 = 4.75 m linear displacement (s) = 70 m The angular displacement (θ) is given by θ = s/r or, θ = 70 m/4.75 m = 14.7 radians Problem 2: Find the linear distance traveled by an object on a circular path of radius 8.25 m with an angular displacement of 0.358 radians. Solution Given radius (r) = 8.25 m angular displacement (θ) = 0.358 radians The linear distance (s) is given by s = rθ = 8.25 m x 0.385 radian = 3.18 m