Angular acceleration is a vector quantity. It has both magnitude and direction. It is analogous to linear acceleration in translational motion. Unlike linear acceleration, a force is not required for angular acceleration. The skater can accelerate her rotation by contracting her arms. Thus, no external torque is necessary. Angular acceleration is fundamental in understanding rotational dynamics and is crucial in various scientific and engineering applications. Many objects in our daily lives exhibit rotational motion, such as spinning tops, wheels, and planets in orbit.
Formula
Instantaneous Angular Acceleration
Relationship with Linear (Tangential) Acceleration
Relationship with Torque and Moment of Inertia
Example Problems
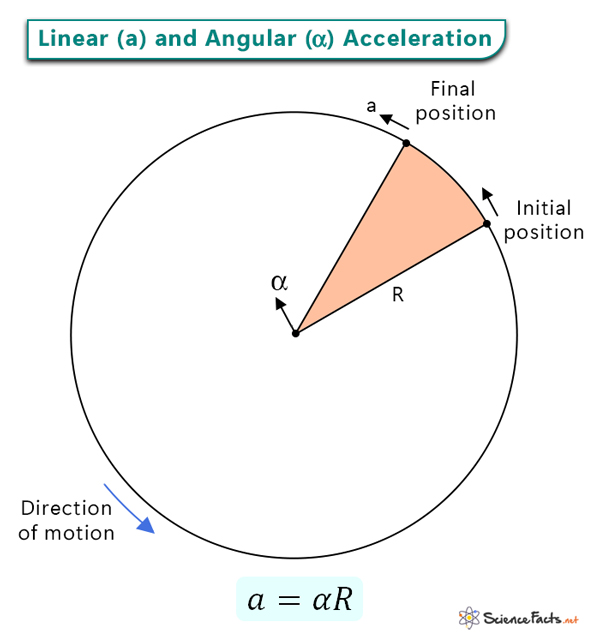
Where ω1 is the initial angular velocity at time t1, and ω2 is the final angular velocity at time t2. Positive angular acceleration implies an increase in angular velocity, while negative angular acceleration indicates a decrease. The angular velocity does not change for uniform circular motion, and the angular acceleration is zero. The direction of the angular acceleration vector is perpendicular to the plane where the rotation takes place. Units and Dimensions The SI unit of angular acceleration is radians per second squared or rad/s2. The dimensional formula is [M0 L0 T-2]. Also, 2π radian = 360°. It can also be written as the double derivative of the angular displacement (θ) since ω = dθ/dt. The relationship between the linear velocity and the angular velocity is Where r is the radial distance of the point under consideration from the origin or the object’s radius. Therefore, Therefore, linear acceleration is the product of the angular acceleration and the radius. Its direction is tangential to the point under consideration and is referred to as the tangential acceleration. Since the linear acceleration and angular acceleration are directly proportional, the greater the angular acceleration, the larger the linear acceleration, and vice versa. The radius also matters. For instance, the smaller a car wheel, the smaller its linear acceleration for a given angular acceleration. The above expression for angular acceleration does not involve time. Objects with high moments of inertia require more torque to achieve a given angular acceleration. For instance, a hollow sphere has a higher moment of inertia than a solid sphere of the same mass and radius. Therefore, rotating it will require more torque to achieve the same angular acceleration as the solid sphere. Given ω1 = 12 rad/s, ω2 = 16 rad/s, and Δt = 1.2 s The angular acceleration is α = (ω2 – ω1)/Δt => α = (16 rad/s – 12 rad/s)/1.2 s => α = 3.33 rad/s2 Problem 2. The front wheel of a motorcycle picks up an angular acceleration of 22 rad/s2 from 0 to 5 seconds. What is its angular velocity? Given α = 22 rad/s2, ω1 = 0, and Δt = 5 s The change in angular velocity is given by Δω = αΔt => ω2 – 0 = 22 rad/s2 x 5 s => ω2 = 110 rad/s