Formula
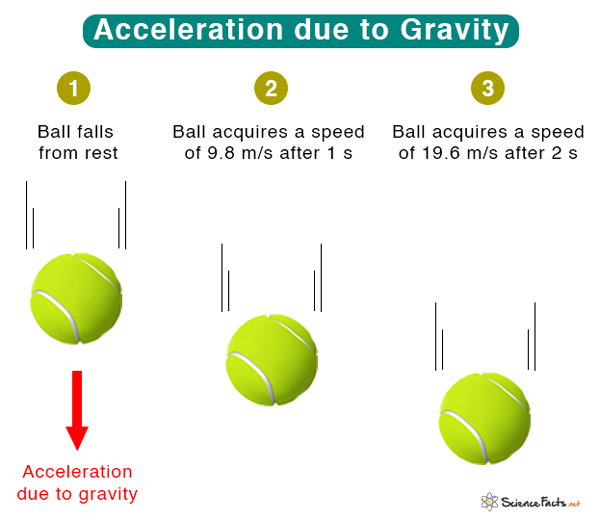
Gravitational Acceleration Value
Factors Affecting Acceleration due to Gravity
Where Fg: Gravitational force M: Mass of the Earth m: Mass of the object R: Radius of the Earth G: Universal gravitational constant From Newton’s second law, the force on an object due to Earth’s gravitation is Comparing the above two equations: Units of g
SI unit: meters per second squared or m/s2cgs unit: centimeters per second squared or cm/s2Imperial unit: feet per second squared or ft/s2
We can make the following conclusions from the above expression:
All bodies experience the same acceleration due to gravity, irrespective of their masses.The acceleration value depends on Earth’s mass, not the object’s mass.
Plugging in the values in the expression for g, we get g = 6.67 x 10-11 Nm2/kg2 x (6 x 1024 kg/6.4 x 106 m)2 => g = 9.8 m/s2 The above value is calculated for the metric system of units. In the imperial unit, 1 m = 3.28 ft. Therefore, g = 32.14 ft/s2. At a height h from Earth’s surface, this equation modifies to Therefore, by repeating the same steps as above, we get Since GM/R2 is the acceleration g on the Earth’s surface The above expression is the acceleration due to gravity at a height above Earth’s surface. By examining the formula, we can say that acceleration decreases with an increase in the height of an object and becomes zero at an infinite distance from the Earth. Note that when h « R, the expression reduces to
2. Depth Below the Surface of the Earth
Recall the expression for acceleration due to gravity at the surface of the Earth Earth’s mass M can be written in terms of density ρ and volume (\frac{4}{3}\pi R^3 ). Therefore, At a distance d below the Earth’s surface, the acceleration due to gravity is given by Diving one equation by the other Note that at the Earth’s surface, d = 0 and gd = g
3. Latitude
Suppose an object with mass m lies on the Earth’s surface at a latitude θ. Let ω bet the angular velocity of the Earth. For the non-inertial frame, there exists a centrifugal force on the object given by Where r is the shortest distance of the object from the axis of Earth’s rotation. It is also the radius of the circular path that the object traces. The gravitational force is The two co-planer forces will add vectorially to give the resultant force on the object. When two co-planer vectors form two sides of a parallelogram, the resultant vector is given by its diagonal. According to the parallelogram law of vector addition, the magnitude of the apparent gravitational force mg’ at a latitude θ is (mg’)2 = (mg)2 + (mrω2)2 + 2 (mg) (mrω2) cos (180 – θ) … The relationship between r and Earth’s radius R is r = R cos θ Substituting for r, we get g’ = g – Rω2cos2θ Here, g′ is the apparent value of acceleration due to gravity at a latitude θ due to Earth’s rotation, and g is the actual value of gravity at the same latitude without considering Earth’s rotation. At the equator, θ = 0. Therefore, g’ = g – Rω2 At the poles, θ = ± 90. Therefore, g’ = g We can conclude that the acceleration due to gravity at the poles is more than at the equator.